如何读取协方差矩阵

协方差是衡量一个变量的变化与第二个变量的变化如何关联的指标。更具体地说，它是两个变量线性相关程度的度量。

协方差矩阵是一个方阵，显示许多不同变量之间的协方差。这是了解数据集中不同变量如何关联的有用方法。

以下示例展示了如何在实践中读取协方差矩阵。

如何读取协方差矩阵

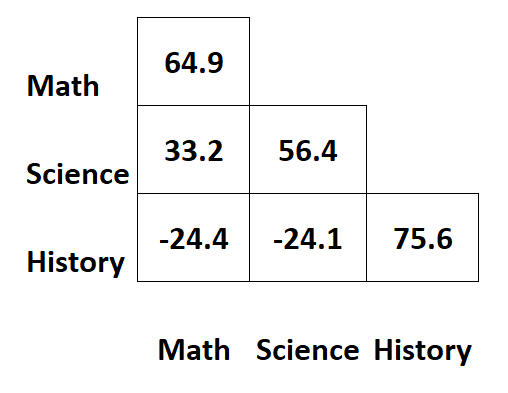
假设我们有以下协方差矩阵，其中包含有关学生三个不同科目的考试成绩的信息：

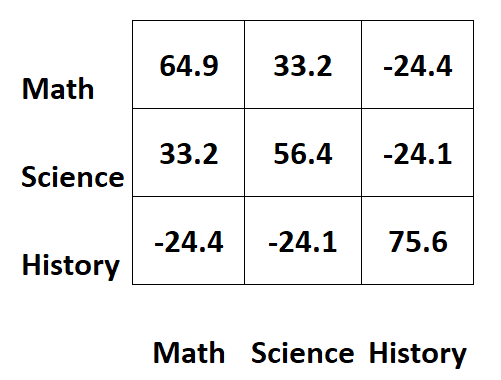
矩阵对角线上的值代表每个受试者的方差。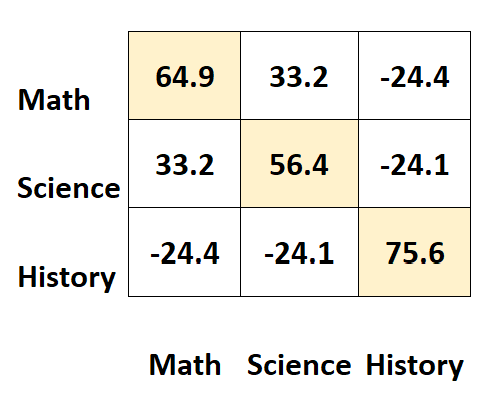

例如：

• 数学结果的方差为64.9 。
• 科学分数的方差是56.4 。
• 历史分数的方差为75.6 。

矩阵的其他值代表不同主体之间的协方差。

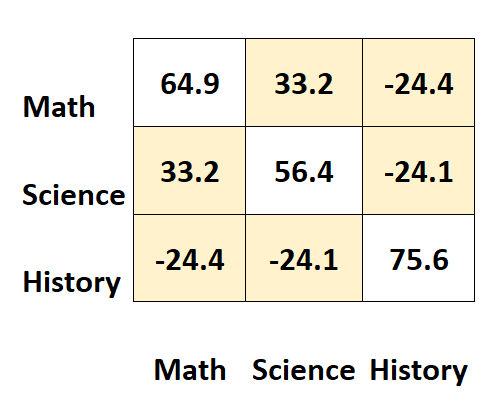
例如：

• 数学和科学分数之间的协方差为33.2 。
• 数学和历史分数之间的协方差为–24.4 。
• 科学和历史分数之间的协方差为–24.1 。

协方差为正数表示两个变量倾向于同时增加或减少。

例如，数学和科学具有正协方差 ( 33.2 )，表明数学得分高的学生也往往在科学得分高。

相反，数学成绩不佳的学生在科学方面也往往表现不佳。

协方差为负数表示随着一个变量的增加，第二个变量趋于减少。

例如，数学和历史具有负协方差 ( -24.44 )，表明数学成绩较高的学生往往在历史成绩较低。

相反，数学成绩低的学生往往历史成绩高。

关于协方差矩阵对称性的注解

需要注意的是，协方差矩阵是完全对称的。

例如，右上角的单元格显示与左下角单元格完全相同的值：

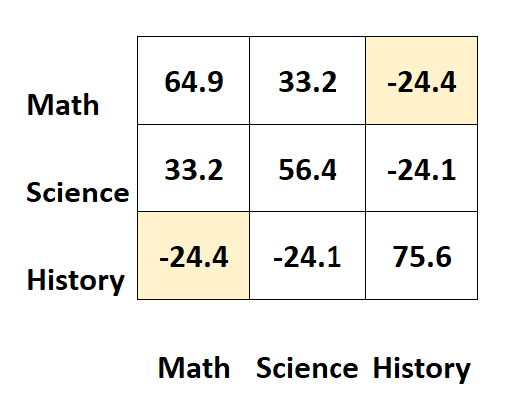
事实上，这两个单元测量了历史和数学之间的协方差。

由于协方差矩阵是对称的，因此矩阵中显示的协方差值有一半是多余且不必要的。

因此，有时只会显示一半的协方差矩阵：

何时使用协方差矩阵

在实践中，您通常需要比协方差矩阵更频繁地创建和解释相关矩阵。

然而，协方差矩阵通常“在幕后”用于不同的机器学习算法和模型。

例如，在主成分分析过程中使用协方差矩阵，这有助于我们理解包含大量变量的数据集中的底层模式。

其他资源

以下教程解释了如何使用不同的统计软件创建协方差矩阵：

如何在 R 中创建协方差矩阵
如何在 Python 中创建协方差矩阵
如何在 SPSS 中创建协方差矩阵
如何在 Excel 中创建协方差矩阵