如何阅读带有异常值的箱线图（附示例）

箱线图是一种显示数据集五位数字摘要的图，其中包括：

• 最小值
• 第一个四分位数（第 25 个百分位数）
• 中值
• 第三个四分位数（第 75 个百分位数）
• 最大值

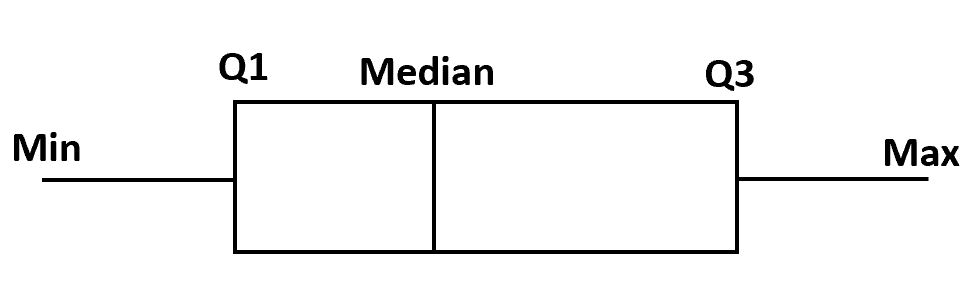
为了制作箱线图，我们首先从第一四分位数到第三四分位数绘制一个箱线。

接下来，我们在中线处画一条垂直线。

最后，我们绘制四分位数的“须线”，直到最小值和最大值。

在大多数统计软件中，如果观测值满足以下两个要求之一，则将其定义为异常值：

• 观测值是第一个四分位数 (Q1) 以下四分位数间距的 1.5 倍
• 观测值是第三个四分位数 (Q3) 上方四分位数间距的 1.5 倍。

如果数据集中存在异常值，通常会在箱线图中用须线范围之外的小点进行标记：

发生这种情况时，箱线图中的“最小值”和“最大值”分别简单地指定为 Q1 – 1.5*IQR 和 Q3 + 1.5*IQR 的值。

以下示例显示如何解释带有和不带有异常值的箱线图。

示例：解释带有离群值的箱线图

假设我们创建以下两个箱线图来可视化来自两个不同球队的篮球运动员的得分分布：

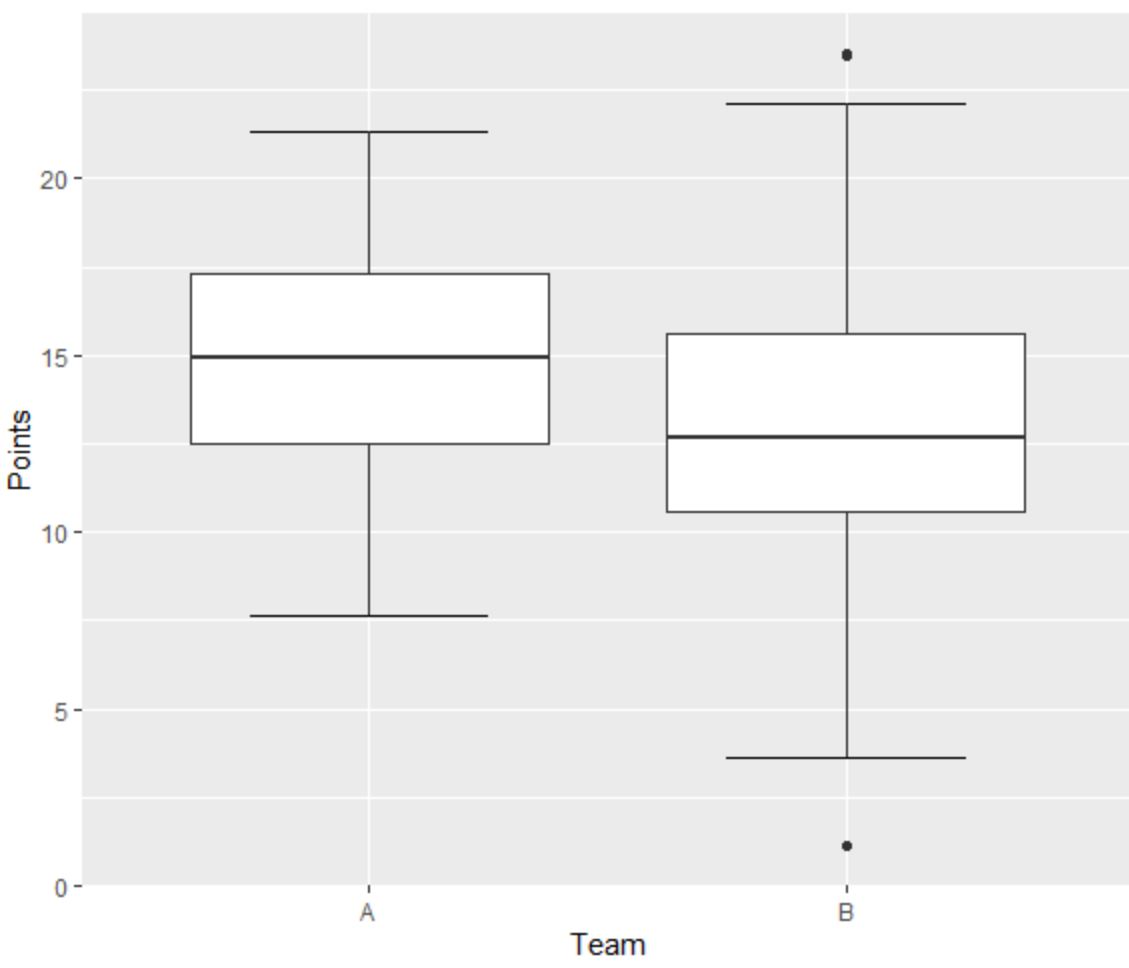
A 队的左侧箱线图没有异常值，因为最小或最大须线之外没有小点。

然而，B 队的右侧箱线图有一个高于“最大值”值的离群值和一个低于“最小值”值的离群值。

以下是 B 队“积分”变量分布的当前五位数字摘要：

• 最小值：1.1
• 第一个四分位数：10.5
• 中位数：12.7
• 第三个四分位数：15.6
• 最大值：23.5

以下是计算潜在异常值限制的方法：

四分位数刻度：第三个四分位数 – 第一个四分位数 = 15.6 – 10.5 = 5.1

下限：Q1 – 1.5*IQR = 10.5 – 1.5*5.1 = 2.85

上限：Q3 + 1.5*IQR = 15.6 + 1.5*5.1 = 23.25

箱线图中最小值和最大值的须线放置在2.85和23.25处。

因此，值为1.1和23.5的观测值都属于箱线图中的异常值，因为它们超出了下限和上限。

额外奖励：下面是我们用 R 编程语言创建这两个箱线图的确切代码：

 library (ggplot2)

#make this example reproducible 
set. seeds (2)

#create data frame
df <- data. frame (Team = factor(rep(c("A", "B"), each = 200)), 
                 Points = c(rnorm(200, mean = 15, sd = 3), 
                           rnorm(200, mean = 12, sd = 4))) 

#create box plots
ggplot(df, aes(x = Team, y = Points)) +
  stat_boxplot(geom = " errorbar ", width = 0.5) +  
  geom_boxplot() 

#calculate summary statistics for each team
tapply(df$Points, df$Team, summary)

其他资源

以下教程提供有关箱线图的其他信息：

如何比较箱线图
如何识别箱线图中的不对称性
如何找到箱线图的四分位数范围