如果统计数据具有弹性意味着什么？
如果统计数据对极值不敏感，则称其具有弹性。
以下是弹性统计的两个示例：
- 中位数
- 四分位数范围
以下是不成立的统计数据示例：
- 平均
- 标准差
- 整齐的
以下示例说明了弹性统计数据和非抵抗统计数据之间的差异。
示例：抗性和非抗性统计
假设我们有以下数据集：
数据集： 2、5、6、7、8、13、15、18、22、24、29
使用计算器或统计软件，我们可以计算该数据集的以下持有统计值：
- 中位数：13
- 四分位数间距：13.5
我们还可以计算该数据集的以下非弹性统计数据的值：
- 平均分：13.54
- 标准差：8.82
- 范围：27
现在考虑该数据集是否添加了极端异常值：
数据集： 2、5、6、7、8、13、15、18、22、24、29、450
我们可以再次计算该数据集的以下弹性统计数据的值：
- 中位数：14
- 四分位数间距：15.75
我们还可以计算该数据集的以下非弹性统计数据的值：
- 平均分：49.92
- 标准差：126.27
- 范围：448
请注意，通过简单地向数据集添加极值，非阻力统计数据发生了多大变化：
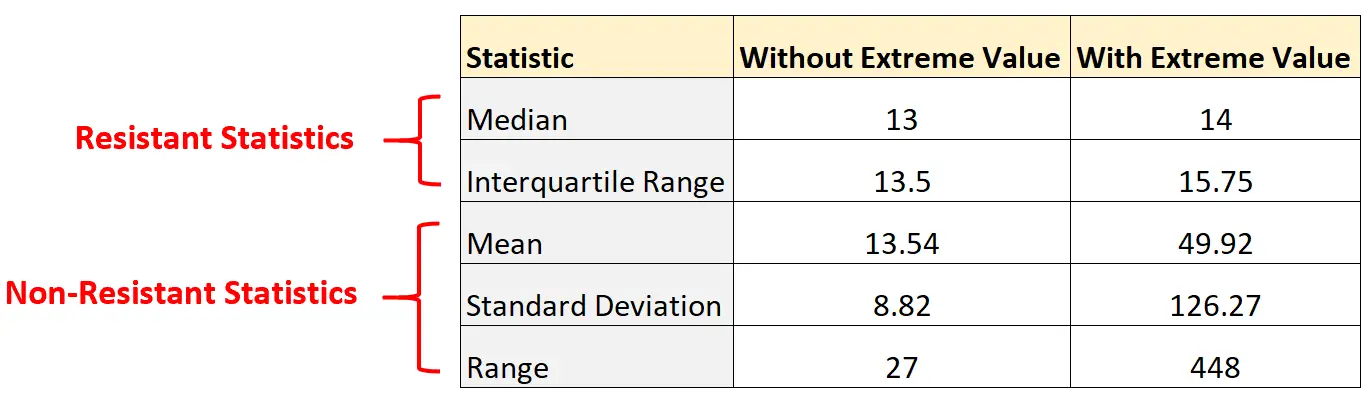
相反，抵抗战士的统计数据几乎没有变化。中位数和四分位数间距仅略有变化。
何时使用弹性统计数据
衡量数据集中值的中心和离散度的最常用统计数据分别是均值和标准差。
不幸的是，这两个统计数据都对极值敏感。因此，如果数据集中存在异常值，平均值和标准差将无法准确描述数据集中值的分布。
相反，如果存在异常值，建议使用中位数和四分位数范围来衡量数据集中值的中心和离散度，因为这两种统计数据都是稳健的。
其他资源
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多