威布尔分布
本文解释了什么是威布尔分布及其用途。此外,您将能够看到威布尔分布的图形表示以及这种类型的概率分布的属性。
什么是威布尔分布?
威布尔分布是由两个特征参数定义的连续概率分布:形状参数 α 和尺度参数 λ。
在统计学中,威布尔分布主要用于生存分析。同样,威布尔分布在不同领域有许多应用。我们将在下面详细介绍如何使用威布尔分布。
![]()
据作者介绍,威布尔分布也可以用三个参数进行参数化。然后,添加第三个参数,称为阈值,该参数指示分布图开始的横坐标。
威布尔分布以瑞典人 Waloddi Weibull 的名字命名,他在 1951 年对其进行了详细描述。然而,威布尔分布是由 Maurice Fréchet 于 1927 年发现的,并由 Rosin 和 Rammler 于 1933 年首次应用。
绘制威布尔分布图
一旦我们了解了威布尔分布的定义,我们就会看到它的图形表示如何根据其参数值而变化。
下面您可以看到几个示例,说明威布尔分布的密度函数图如何根据形状参数和尺度参数的值而变化。
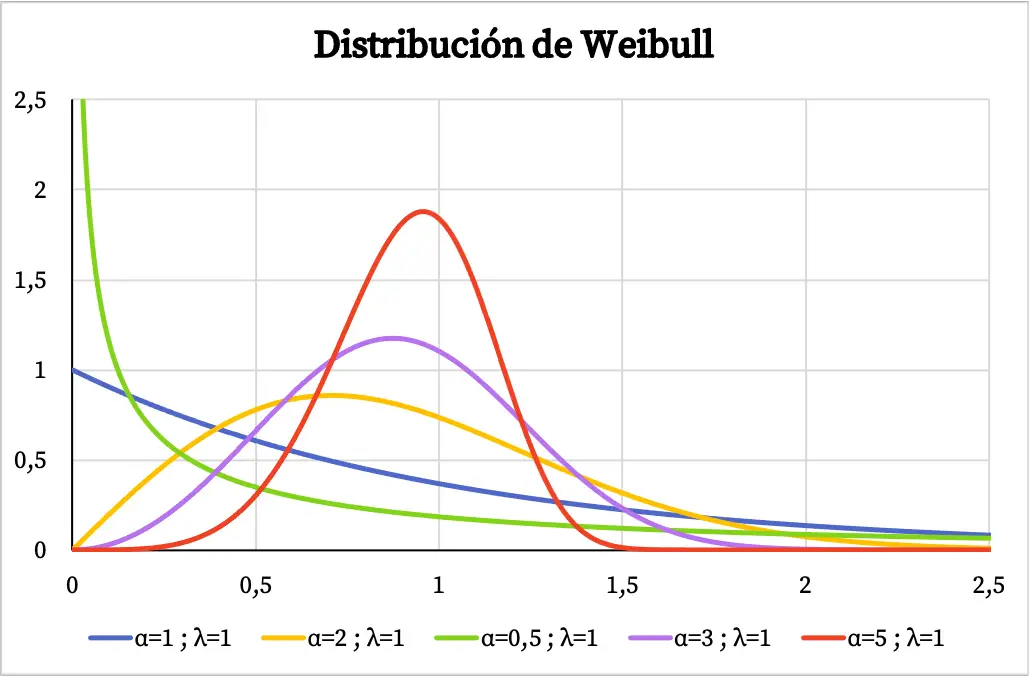
当使用威布尔分布对系统故障率随时间的变化进行建模时,形状参数 α 的值含义如下:
- α<1:故障率随着时间的推移而降低。
- α=1:故障率随时间保持恒定。
- α>1:故障率随时间增加。
另一方面,在下图中,您可以看到根据其特征值绘制的威布尔分布的累积概率函数。
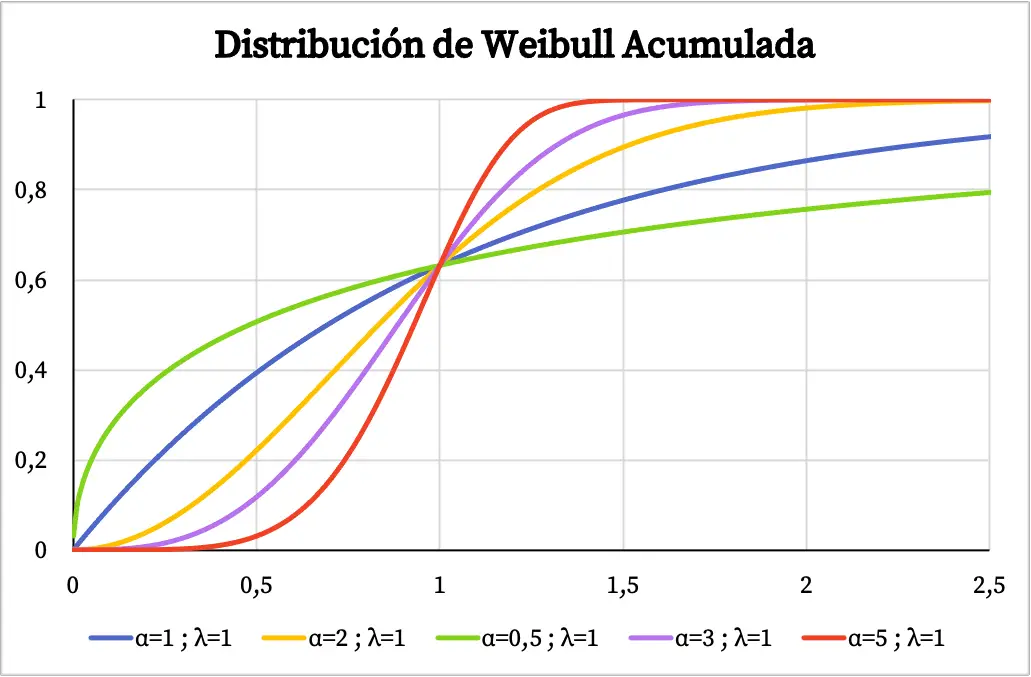
威布尔分布的特征
威布尔分布具有以下特点:
- 威布尔分布有两个定义其图形的特征参数:形状参数 α 和尺度参数 λ。两个参数都是正实数。
![\begin{array}{c}\alpha >0\\[2ex]\lambda >0\\[2ex]\text{Weibull}(\alpha,\lambda)\end{array}” title=”Rendered by QuickLaTeX.com” height=”92″ width=”101″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li>威布尔分布仅接受正横坐标值。</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-c8794febbd607514546841a325490654_l3.png)
![]()
- 威布尔分布的平均值通过以下公式计算:
![]()
- 另一方面,求威布尔分布方差的公式为:
![]()
- 服从 α>1 的威布尔分布的随机变量的众数可以由以下表达式确定:
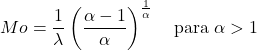
![]()
- 类似地,威布尔分布的累积概率函数的公式为:
![]()
- 威布尔分布的不对称系数通过以下公式计算:
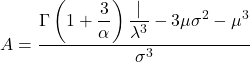
- 最后,可以确定威布尔分布峰度系数的公式如下:
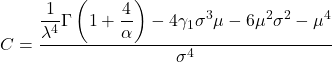
金子
![]()
威布尔分布的应用
威布尔分布有许多应用,包括:
- 在应用统计学中,威布尔分布用于生存分析。
- 在工程中,威布尔分布用于对与制造时间相关的函数进行建模。
- 在雷达系统中,模拟接收信号的色散。
- 在保险领域,对索赔范围进行建模。
- 例如,在气象学中,对不同风速的频率进行建模。