学生 t 检验
本文解释了什么是学生 t 检验以及它在统计学中的用途。因此,您将了解如何进行 Student t 检验、Student t 检验有哪些不同类型以及每种类型的公式。
什么是学生 t 检验?
学生 t 检验,也称为T 检验或简称t 检验,是一种统计检验,其中检验统计量遵循学生 t 分布。因此,在统计学中,学生 t 检验用于拒绝或接受假设检验的原假设。
具体来说,学生 t 检验用于假设检验,其中所研究的总体遵循正态分布,但样本量太小而无法了解总体方差。
简而言之,Student’s t 检验用于拒绝或接受某些假设检验的研究假设。例如,学生 t 检验用于检验一个样本、独立样本或相关样本的假设。然后我们将了解如何计算每种情况下的学生 t 检验。
学生 t 检验的类型
学生 t 检验分为三种类型:
- 单样本学生 t 检验– 用于检验有关样本均值的假设。
- 两个独立样本的学生 t 检验:它允许您检验两个独立样本均值之间差异的假设。
- 两个配对样本(或相关样本)的学生 t 检验– 用于调查有关两次测试样本平均值的假设。
学生 t 检验样本
样本均值的假设检验是指检验的原假设和备择假设说明总体均值的值的情况。
单样本学生 t 检验的公式如下:

金子:
-

是平均值的假设检验统计量,由学生 t 分布定义。
-

是样本均值。
-

是假设检验中提出的平均值。
-

是样本标准差。
-

是样本大小。
计算出学生 t 检验的值后,必须将具有临界值的统计检验结果解释为是否拒绝原假设:
- 如果均值的假设检验是双向的,并且学生 t 检验的绝对值大于临界值 t α/2|n-1 ,则拒绝原假设。
- 如果均值的假设检验与右尾匹配,并且学生的 t 检验值大于临界值 t α|n-1 ,则拒绝原假设。
- 如果平均值的假设检验与左尾匹配,并且学生的 t 检验值小于临界值 -t α|n-1 ,则拒绝原假设。
![Rendered by QuickLaTeX.com \begin{array}{l}H_1: \mu\neq \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |t|>t_{\alpha/2|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu> \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t>t_{\alpha|n-1} \text{ se rechaza } H_0\\[3ex]H_1: \mu< \mu_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } t<-t_{\alpha|n-1} \text{ se rechaza } H_0\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-31fb206b75a47181c7c673f54ba28ee8_l3.png)
请注意,关键测试值是从学生分布表中获得的。
独立样本的学生 t 检验
独立样本的学生 t 检验用于拒绝或接受两个总体均值之间存在关系的假设,例如两个总体的均值不同或总体 A 的均值大于。人口 B .
但是,在这种情况下,学生 t 检验公式会根据总体方差是否可以假设相等而变化。然后我们将看到两种可能的情况。
未知且相等的偏差
当总体方差未知但假设相等时,计算独立样本的 Student t 检验的公式如下:

金子:
-

是方差未知的均值差值的假设检验统计量,遵循自由度为 n 1 + n 2 -2 的 Student t 分布。
-

是总体 1 的平均值。
-

是总体 2 的平均值。
-

是样本 1 的平均值。
-

是样本 2 的平均值。
-

是汇总标准差。
-

是样本量 1。
-

是样本量 2。
使用以下公式计算两个样本的组合标准差:

未知和不同的变化
当总体方差未知且假设不同时,独立样本的 Student t 检验计算公式如下:

金子:
-

是方差未知的均值差值的假设检验统计量,遵循 Student t 分布。
-

是总体 1 的平均值。
-

是总体 2 的平均值。
-

是样本 1 的平均值。
-

是样本 2 的平均值。
-

是总体 1 的标准差。
-

是总体 2 的标准差。
-

是样本量 1。
-

是样本量 2。
但是,在这种情况下,Student t 分布的自由度使用以下公式计算:

配对或相关样本的学生 t 检验
当所研究的两个样本彼此相关时使用此检验,因此它实际上是已分析两次的个体的单个样本(每次在不同的条件下)。
例如,您可以分析学生在数学和统计学课程中的成绩,看看两个科目的平均值之间是否存在显着差异。在这种情况下,每个学生的数学成绩都与该学生的统计成绩相关联。
配对或相关样本的学生 t 检验公式为:
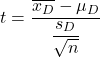
金子:
-

是配对均值的假设检验统计量,由学生 t 分布定义。
-
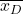
是由数据差异形成的样本的平均值。
-
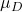
是假设检验中提出的平均值。
-
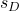
是由数据差异形成的样本的标准差。
-

是样本大小。
学生的 t 检验假设
为了进行学生 t 检验,必须满足以下条件:
- 连续性——样本数据是连续的。
- 随机性:数据样本是随机选择的。
- 同质性:数据样本的方差是同质的。
- 正态性——定义数据样本的分布近似正态。
如何进行学生 t 检验
最后,总而言之,详细介绍了执行学生 t 检验所需遵循的步骤。