实验概率

在这里您将了解实验概率的含义以及实验概率的计算方法。此外，您将能够看到计算实验概率的分步解决示例。

什么是实验概率？

实验概率是基于实验结果或经验事实的统计度量，表示事件发生的概率。

而且，实验重复次数越多，得到的实验概率就越精确。因此，通常使用能够快速模拟数千次实验的计算机程序来确定实验概率，从而获得更好的精度。

实验概率也称为经验概率或频率概率。

实验概率是0到1之间的数字。从逻辑上讲，一个事件的实验概率值越大，发生的可能性越大，反之，值越小，发生的可能性越小。有可能发生。或事件发生。但实验概率的值总是在零和一之间。

实验概率公式

实验概率的公式是实验期间事件发生的次数除以实验执行的总次数。

例如，如果一个人向一个目标扔了 10 个飞镖，并成功击中了中心的 6 个飞镖，则该人击中中心的概率如下：

实验概率示例

一旦我们了解了实验概率的数学定义，我们就会解决此类概率的分步练习。目的是让您了解如何计算事件的实验概率，因此如果您有任何疑问，可以在评论中写下。

• 计算构成掷骰子随机实验的基本事件的实验概率。

在求实验概率之前，我们先计算理论概率，将得到的实验结果与理论结果进行比较。众所周知，掷骰子时有六种可能的结果（1、2、3、4、5和6），因此每个基本事件的理论概率为：

为了解决这个练习，我们必须模拟几次掷骰子并将结果记录在列联表中。在本例中，我们将使用 Excel 程序进行模拟，但您显然可以使用您选择的程序。

我们将首先模拟十次投掷，然后模拟一百次投掷，最后模拟一千次投掷。这样我们就能够分析结果并了解它们如何根据实验的样本量而变化。随机模拟10次掷骰子后得到的结果如下：

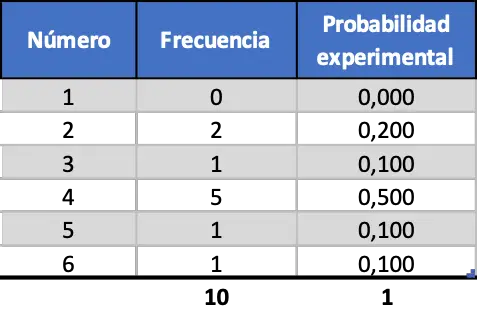
正如您所看到的，目前获得的实验概率与之前计算的理论概率（0.167）有很大差异。

但随着我们增加测试次数，这两个指标变得更加相似，看一下 100 次启动的模拟：

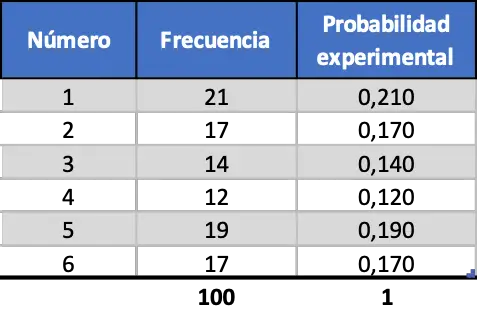
现在实验概率看起来更像理论概率值，但是，我们仍然得到遥远的值。

最后，我们执行相同的过程，但模拟 1000 次启动：

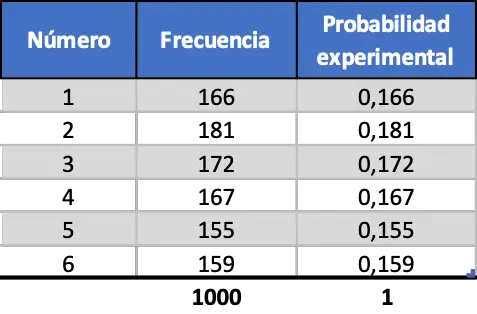
正如您在最后一个列联表中看到的，现在实验概率的值与理论概率非常相似。

综上所述，进行的实验次数越多，某个事件的实验概率值就越接近其理论概率。这个规则被定义为大数定律，即数据越多，实验值就越接近理论值。

同样，如果您比较三个频率表，您会发现实验概率不是确定的，而是根据进行的实验数量而变化。这意味着您必须知道如何解释获得的值。

实验概率和理论概率

实验概率和理论概率（或经典概率）之间的区别在于，实验概率是根据实际实验收集的数据计算的，而理论概率是在不需要进行任何实验的情况下计算的。

正如我们所看到的，我们必须模拟大量的实验来推断事件的实验概率。然而，计算理论概率涉及理论和逻辑。您可以在这里查看它是如何完成的：