密度函数
在本文中,您将了解什么是密度函数、如何根据密度函数计算概率以及该概率函数的特征。此外,您将能够看到密度函数和分布函数之间的差异。
什么是密度函数?
密度函数,也称为概率密度函数,是描述连续随机变量取某一值的概率的数学函数。
换句话说,与变量相关的密度函数在数学上定义了该变量取值的概率。
例如,假设人口中成年人身高超过1.80 m的概率为35%,那么密度函数在计算该概率时将指示35%的概率。
有时概率密度函数缩写为PDF。
使用密度函数计算概率
为了找到连续变量在区间内取值的概率,有必要计算与该变量相关的密度函数在区间界限之间的积分。
![]()
金子
![]()
是连续随机变量的密度函数。
或者换句话说,变量在某个区间内取值的概率等于该区间内密度函数下的面积。
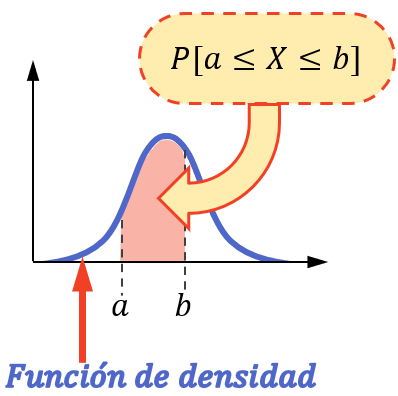
注意,只有当统计变量服从连续分布时,例如正态分布、指数分布、泊松分布等,才能用这种方式进行概率计算。
密度函数的性质
密度函数具有以下性质:
- 对于任何 x 值,密度函数的值为零或正值。
![]()
- 另外,密度函数的最大值等于1。
![]()
- 事实上,无论变量如何,密度函数图下的总面积始终等于 1,因为它对应于所有概率的集合。
![]()
- 如上一节所述,连续变量在某个区间内取值的概率是通过该区间内密度函数的积分来计算的。
![]()
密度函数和分布函数
在最后一节中,我们将看到密度函数和分布函数有何不同,因为它们是通常被混淆的两种类型的概率函数。
从数学上讲,分布函数相当于密度函数 的积分,因此分布函数描述了连续变量的累积概率。
也就是说,任何值的分布函数的图像都等于该变量取该值或更低值的概率。
因此,这两类函数之间的数学关系如下:
![]()
金子
![]()
是密度函数并且
![]()
是分布函数。
请注意密度函数的图形表示如何相对于遵循平均值为 1、标准差为 0.5 的正态分布的变量分布函数而变化:

要了解有关分发功能的更多信息,请单击以下链接:
➤参见:分布函数