Excel 中的对数回归（逐步）

对数回归是一种回归类型，用于对增长或下降首先快速加速然后随着时间的推移减慢的情况进行建模。

例如，下图显示了对数衰减的示例：

对于这种类型的情况，可以使用对数回归很好地对预测变量和响应变量之间的关系进行建模。

对数回归模型的方程采用以下形式：

y = a + b*ln(x)

金子：

• y：响应变量
• x：预测变量
• a、b：描述x和y之间关系的回归系数

以下分步示例展示了如何在 Excel 中执行对数回归。

第 1 步：创建数据

首先，我们为两个变量创建假数据： x和y ：

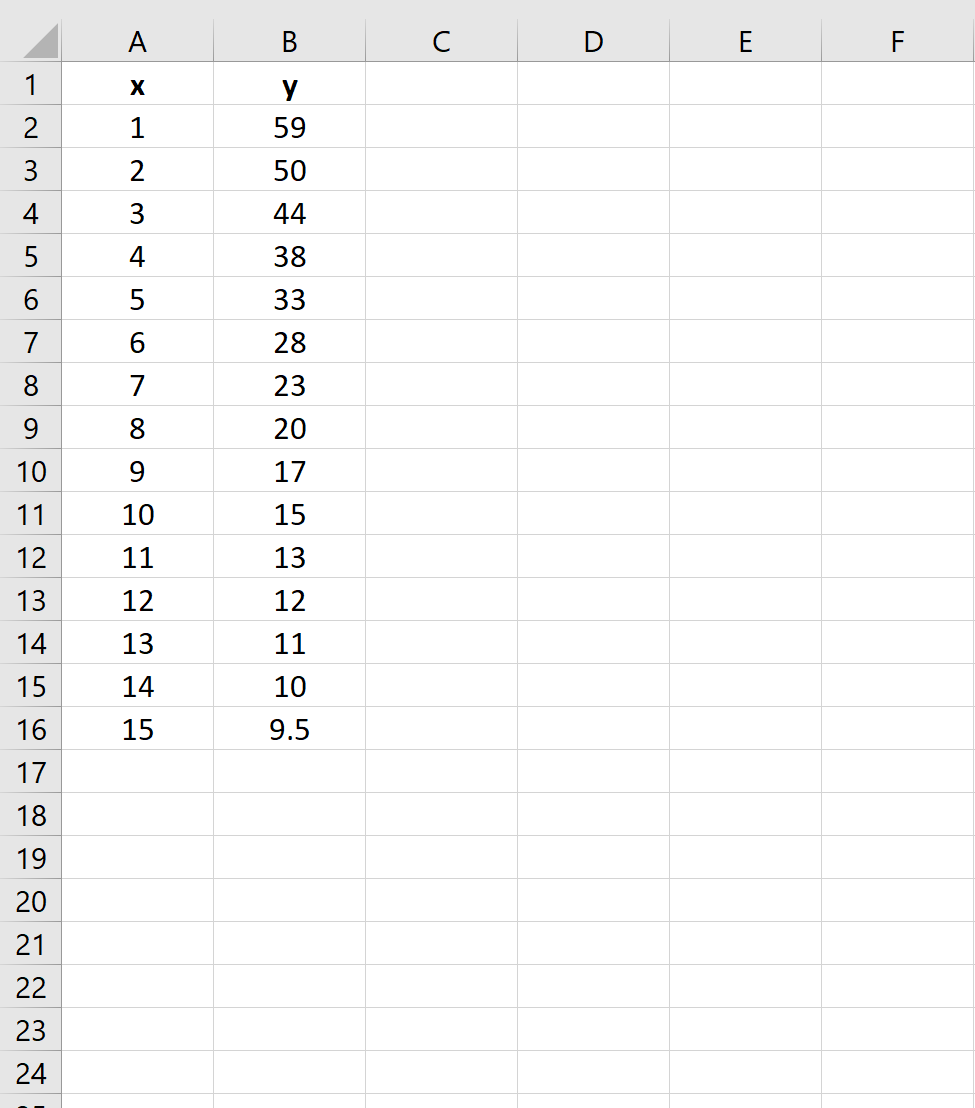
步骤 2：取预测变量的自然对数

接下来，我们需要创建一个新列来表示预测变量x的自然对数：

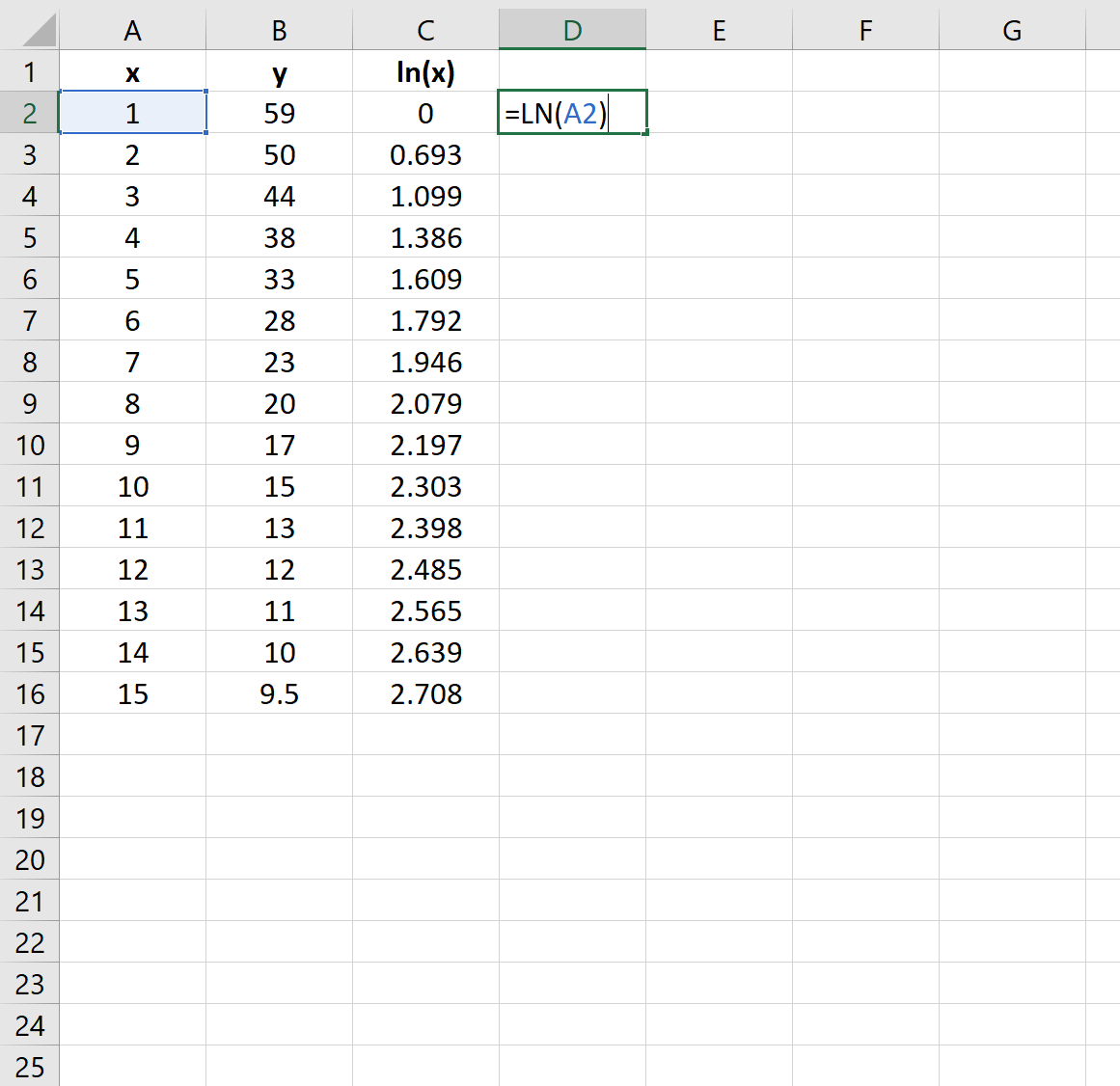
步骤 3：拟合对数回归模型

接下来，我们将拟合对数回归模型。为此，请单击顶部功能区中的“数据”选项卡，然后单击“分析”组中的“数据分析” 。

如果您没有看到数据分析选项，则必须首先加载分析工具库。

在出现的窗口中，单击回归。在出现的新窗口中，提供以下信息：

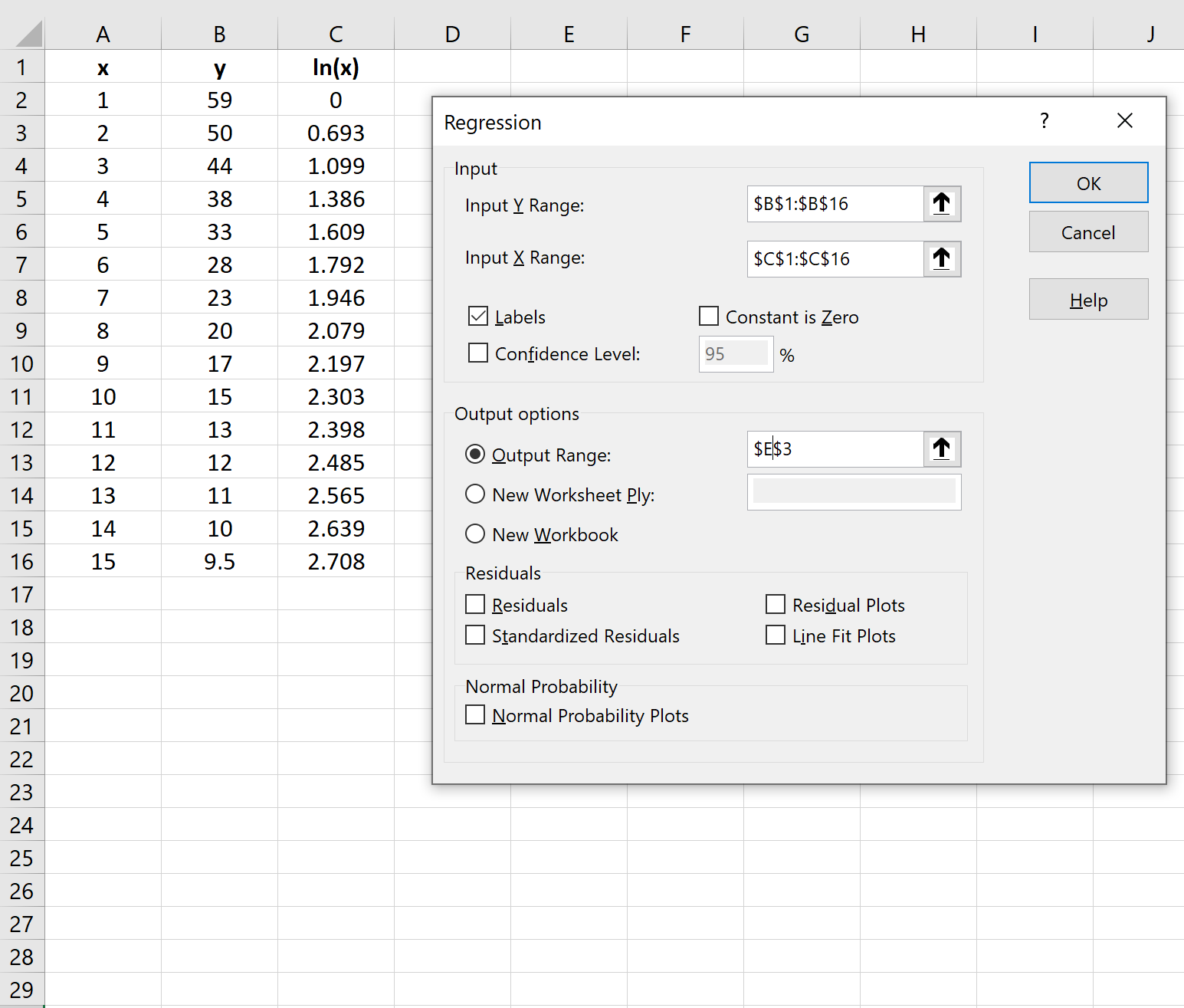
单击“确定”后，将显示对数回归模型的输出：

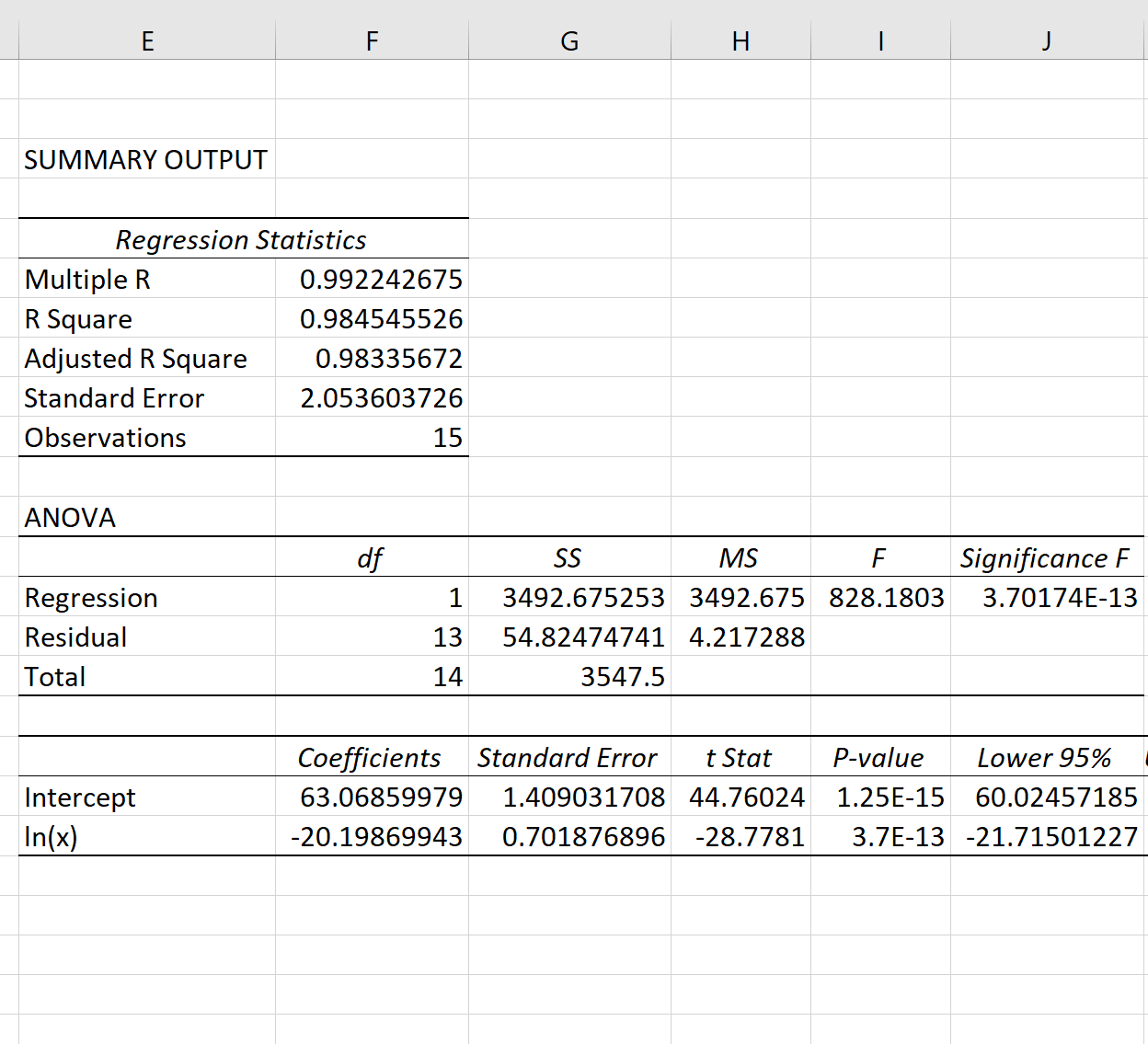
模型的整体 F 值为828.18，相应的 p 值极低（3.70174E-13），表明模型整体上是有用的。

使用输出表中的系数，我们可以看到拟合的对数回归方程为：

y = 63.0686 – 20.1987 * ln(x)

我们可以使用该方程根据预测变量x的值来预测响应变量y 。例如，如果x = 12，那么我们预测y将为12.87 ：

y = 63.0686 – 20.1987 * ln(12) = 12.87

奖励：随意使用此在线对数回归计算器来自动计算给定预测变量和响应变量的对数回归方程。

其他资源

如何在 Excel 中执行简单线性回归
如何在 Excel 中执行多元线性回归
如何在 Excel 中执行多项式回归
如何在 Excel 中执行指数回归