对称分布
在本文中,您将了解什么是对称分布、对称分布的示例以及如何确定分布是对称还是不对称。
什么是对称分布?
在统计学中,对称分布是指均值左侧和均值右侧具有相同数量的值。换句话说,在对称分布中,平均值是对称轴。
例如,正态分布是对称分布。
在所有对称分布中,均值等于中位数。但如果分布也是单峰的(统计模式是单个值),则均值、中位数和众数是等效的。
从逻辑上讲,要充分理解什么是对称分布,您需要清楚什么是均值、中位数和众数。您可以在此处查看这些统计概念的含义:
➤请参阅:什么是均值、中位数和众数?
对称分布的示例
考虑到对称分布的定义,此类分布的示例如下所示:
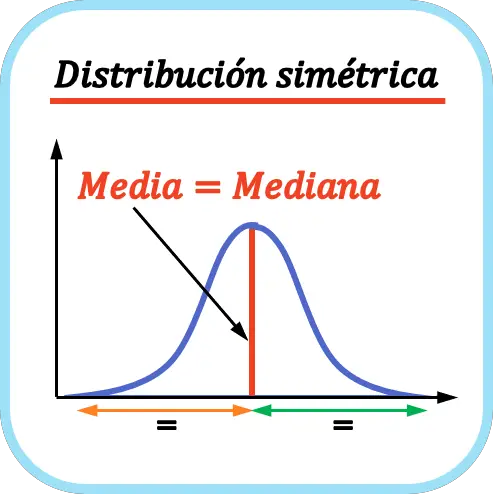
如图所示,分布是对称的,因为均值位于所有数据的中间,即曲线左侧的尾部与右侧的尾部相同。在这种情况下,均值、中位数和众数相同,因为众数是单峰的。
两种不同类型的对称概率分布的两个明显例子是正态分布和均匀分布,因为它们在均值的左侧和右侧具有相同数量的值。
另一方面,分布也可以是对称的和双峰的,即具有两种模式。看下面的例子:
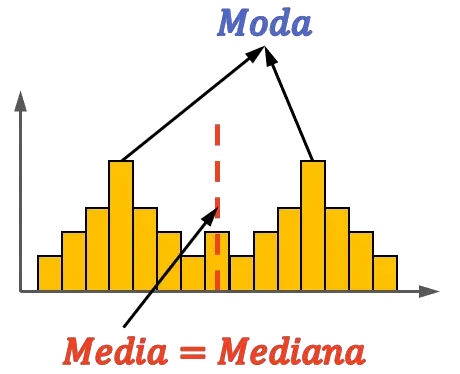
正如您在另一个示例中所看到的,双峰分布也可以是对称的,因为无论其他值如何,它都可以将平均值和中位数放在中心。然而,在这种情况下,众数不一定必须等于均值和众数。
根据对称性的其他类型的分布
除了对称分布之外,还有另外两种类型的非对称分布。
- 对称分布:该分布在均值的左侧和右侧具有相同数量的值。
- 正偏态分布:均值右侧的分布比左侧有更多的不同值。
- 负偏态分布:均值左侧的分布比右侧的不同值更多。

如何判断分布是否对称
为了判断分布是否对称,我们必须计算皮尔逊不对称系数,其公式为:
![]()
金子
![]()
是皮尔逊系数,
![]()
算术平均值,
![]()
模式(统计)和
![]()
标准差。
因此,根据皮尔逊不对称系数的符号,分布将是对称或不对称的:
- 如果皮尔逊偏度系数为正,则意味着分布呈正偏态。
- 如果皮尔逊偏度系数为负,则意味着分布呈负偏态。
- 如果皮尔逊偏度系数为零,则意味着分布是对称的。
但皮尔逊系数只有在分布是单峰的情况下才能计算,否则需要使用Fisher非对称系数,其公式如下:

金子
![]()
算术平均值,
![]()
标准差和
![]()
数据总数。
Fisher 不对称系数的解释与 Pearson 系数相同:如果为正,则表示分布为正不对称;如果为负,则表示分布为负不对称;如果为 0,则表示分布是对称的。