如何在 r 中转换数据(对数、平方根、立方根)
许多统计检验假设响应变量的残差呈正态分布。
然而,残差通常不呈正态分布。解决此问题的一种方法是使用以下三种转换之一来转换响应变量:
1. 对数变换:将响应变量从 y 变换为log(y) 。
2. 平方根变换:将响应变量从 y 变换为√y 。
3. 立方根变换:将响应变量从 y 变换为y 1/3 。
通过执行这些变换,响应变量通常近似正态分布。以下示例展示了如何在 R 中执行这些转换。
R 中的对数变换
以下代码显示如何对响应变量执行日志转换:
#create data frame df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8), x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8), x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7)) #perform log transformation log_y <- log10(df$y)
以下代码显示如何创建直方图来显示执行对数转换之前和之后y的分布:
#create histogram for original distribution hist(df$y, col='steelblue', main='Original') #create histogram for log-transformed distribution hist(log_y, col='coral2', main='Log Transformed')
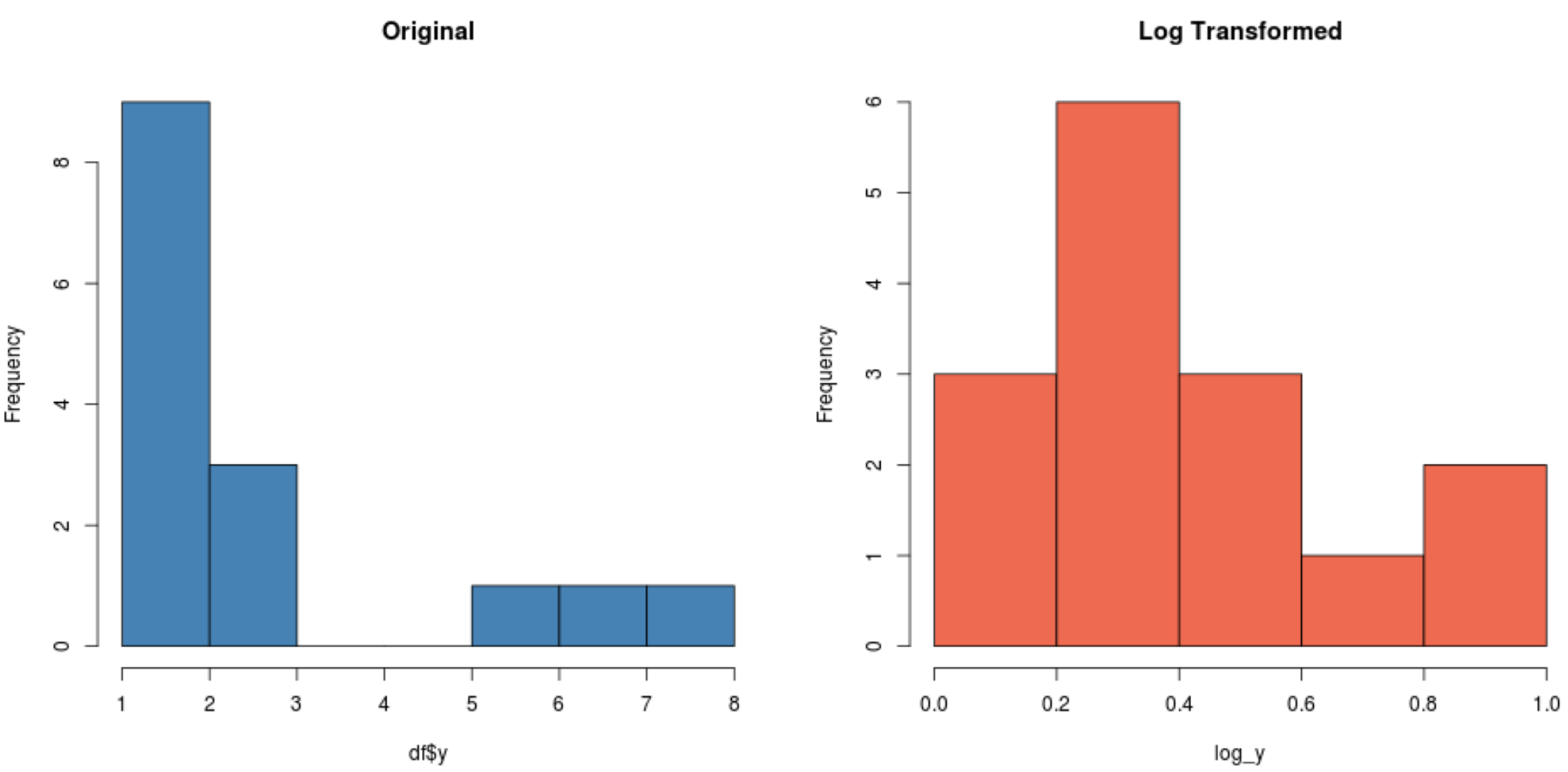
请注意对数变换后的分布比原始分布更加正态。它仍然不是完美的“钟形”,但它比原始分布更接近正态分布。
事实上,如果我们对每个分布进行Shapiro-Wilk 检验,我们会发现原始分布不符合正态性假设,而对数变换分布则不然(α = 0.05 时):
#perform Shapiro-Wilk Test on original data shapiro.test(df$y) Shapiro-Wilk normality test data: df$y W = 0.77225, p-value = 0.001655 #perform Shapiro-Wilk Test on log-transformed data shapiro.test(log_y) Shapiro-Wilk normality test data:log_y W = 0.89089, p-value = 0.06917
R中的平方根变换
以下代码显示如何对响应变量执行平方根变换:
#create data frame df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8), x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8), x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7)) #perform square root transformation sqrt_y <- sqrt(df$y)
以下代码展示了如何创建直方图来显示执行平方根变换之前和之后y的分布:
#create histogram for original distribution hist(df$y, col='steelblue', main='Original') #create histogram for square root-transformed distribution hist(sqrt_y, col='coral2', main='Square Root Transformed')
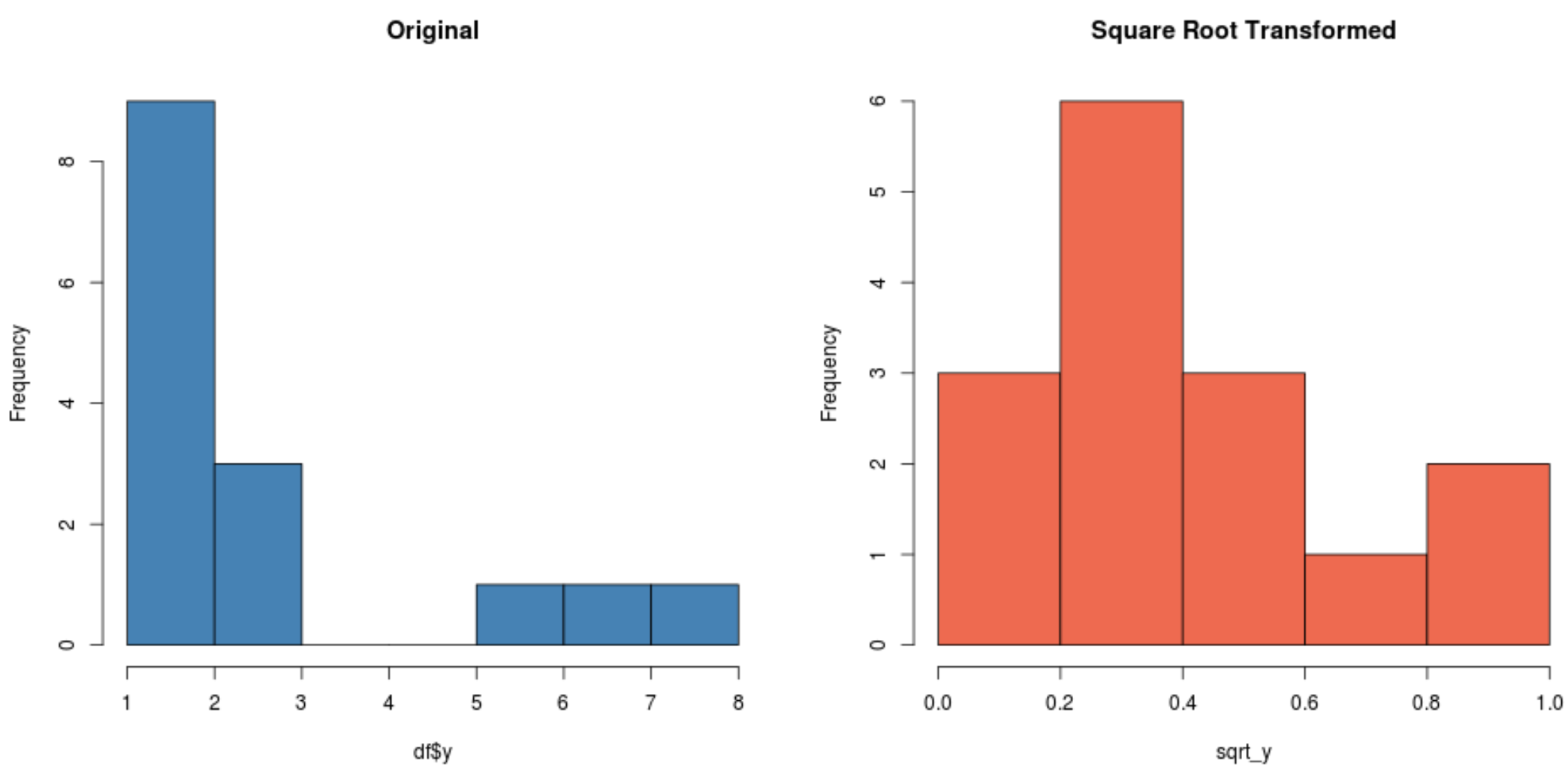
请注意平方根变换后的分布比原始分布更加正态分布。
R中的立方根变换
以下代码显示如何对响应变量执行立方根变换:
#create data frame df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8), x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8), x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7)) #perform square root transformation cube_y <- df$y^(1/3)
以下代码展示了如何创建直方图来显示执行平方根变换之前和之后y的分布:
#create histogram for original distribution hist(df$y, col='steelblue', main='Original') #create histogram for square root-transformed distribution hist(cube_y, col='coral2', main='Cube Root Transformed')
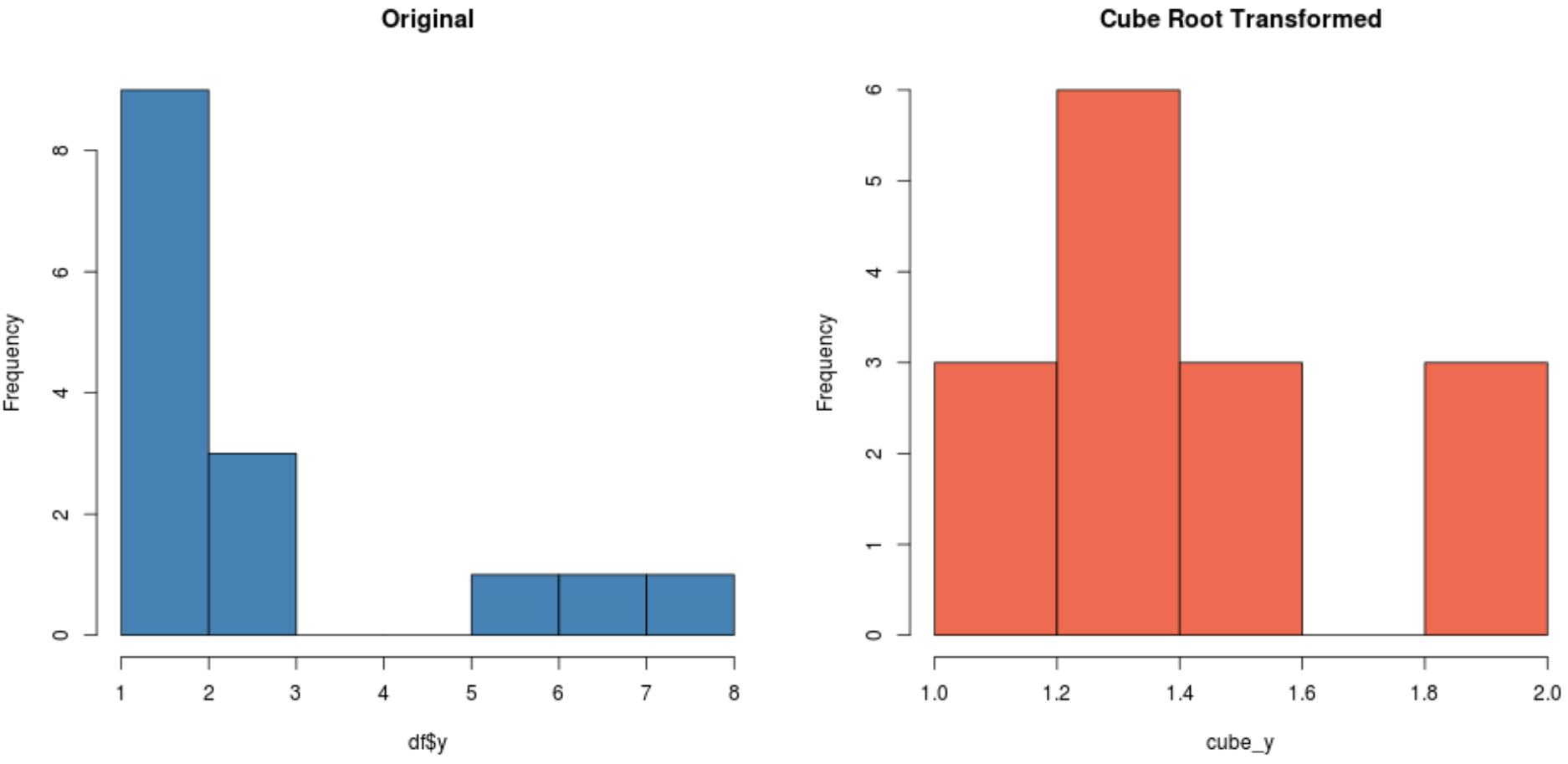
根据您的数据集,这些转换之一可能会生成比其他数据集更呈正态分布的新数据集。