如何在stata中进行层次回归

分层回归是一种我们可以用来比较几种不同线性模型的技术。

基本思想是我们首先用单个解释变量拟合线性回归模型。接下来，我们使用附加解释变量拟合另一个回归模型。如果第二个模型中的 R 平方（响应变量中可由解释变量解释的方差比例）显着高于前一个模型中的 R 平方，则意味着第二个模型更好。

然后，我们重复使用更多解释变量拟合其他回归模型的过程，看看新模型是否比以前的模型有所改进。

本教程提供了如何在 Stata 中执行层次回归的示例。

示例：Stata 中的层次回归

我们将使用一个名为auto 的内置数据集来说明如何在 Stata 中执行层次回归。首先，通过在命令框中键入以下内容来加载数据集：

系统自动使用

我们可以使用以下命令快速汇总数据：

总结一下

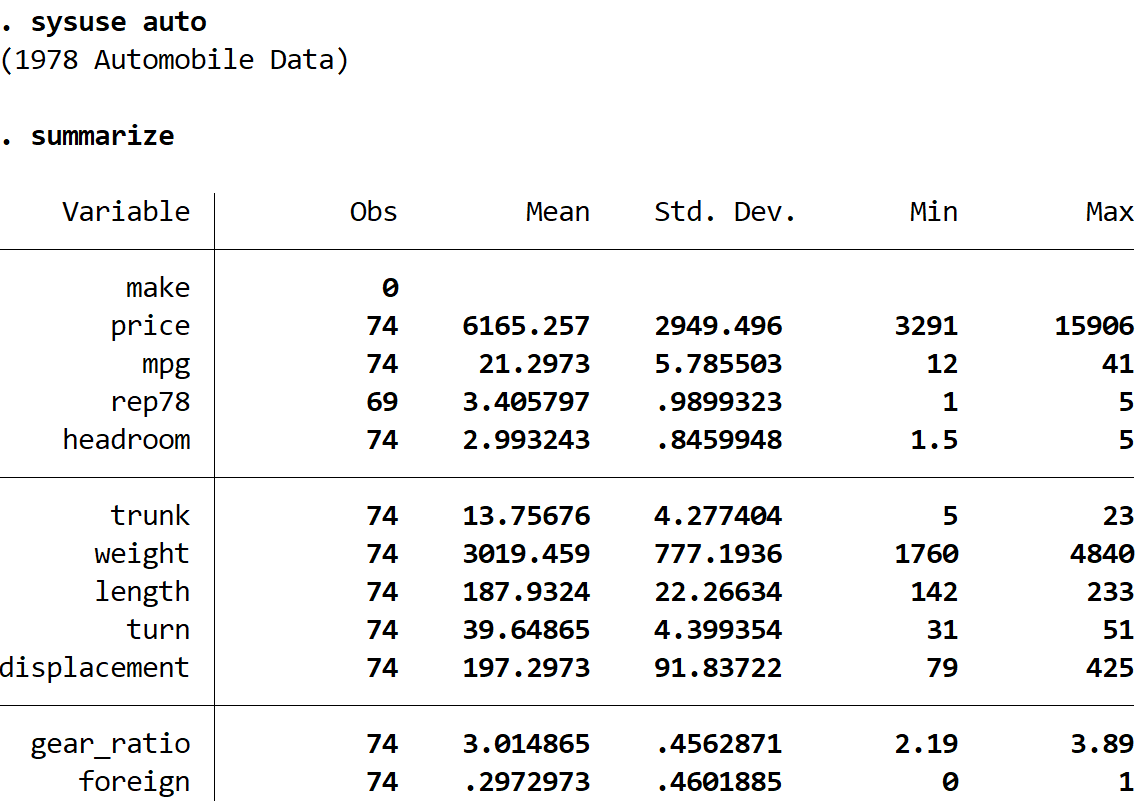
我们可以看到该数据集总共包含 74 辆汽车的 12 个不同变量的信息。

我们将拟合以下三个线性回归模型，并使用层次回归来查看每个后续模型是否比之前的模型提供了显着的改进：

模型1：价格=拦截+英里/加仑

模型2：价格=截距+英里/加仑+重量

模型3：价格=截距+英里/加仑+重量+齿轮比

为了在 Stata 中执行层次回归，我们首先需要安装Hireg软件包。为此，请在命令框中键入以下内容：

找到希雷格

在出现的窗口中，单击https://fmwww.bc.edu/RePEc/bocode/h 中的 Hireg

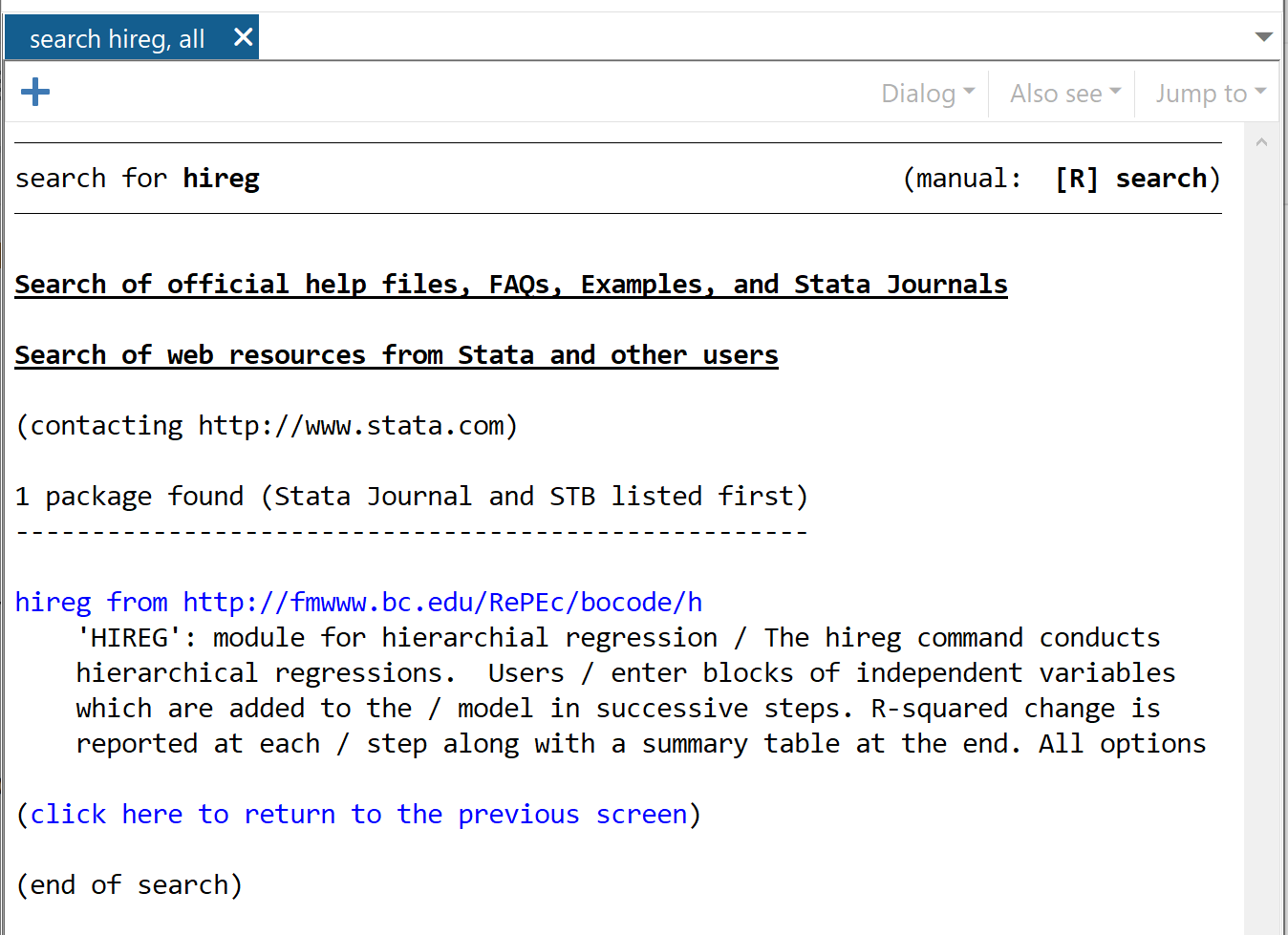
在下一个窗口中，单击显示“单击此处安装”的链接。

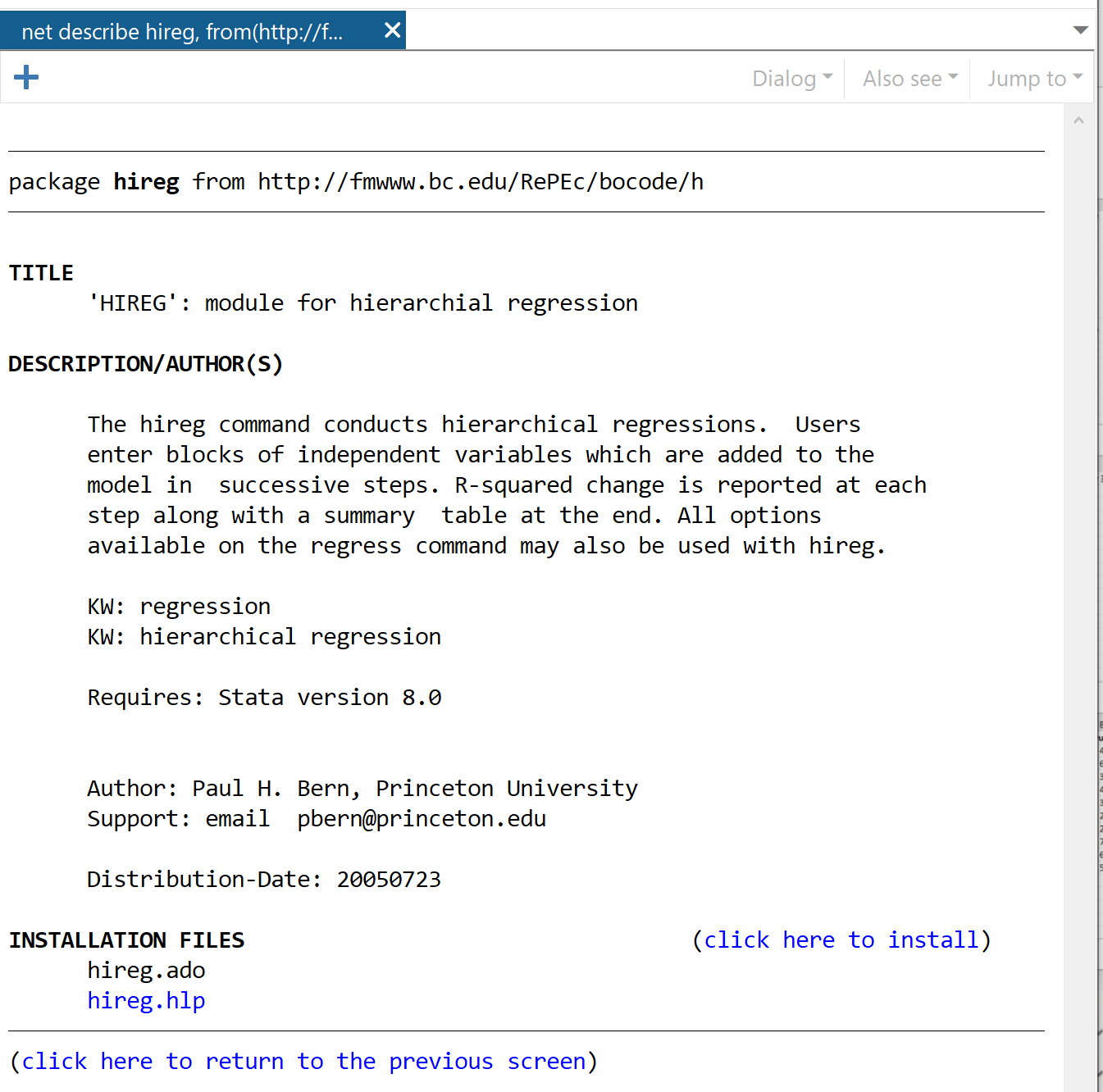
该软件包将在几秒钟内安装。然后，要执行层次回归，我们将使用以下命令：

租赁价格（英里/加仑）（重量）（齿轮比）

这就是 Stata 要做的事情：

• 使用价格作为每个模型中的响应变量执行分层回归。
• 对于第一个模型，使用mpg作为解释变量。
• 对于第二个模型，添加权重作为附加解释变量。
• 对于第三个模型，添加gear_ratio作为另一个解释变量。

这是第一个模型的结果：

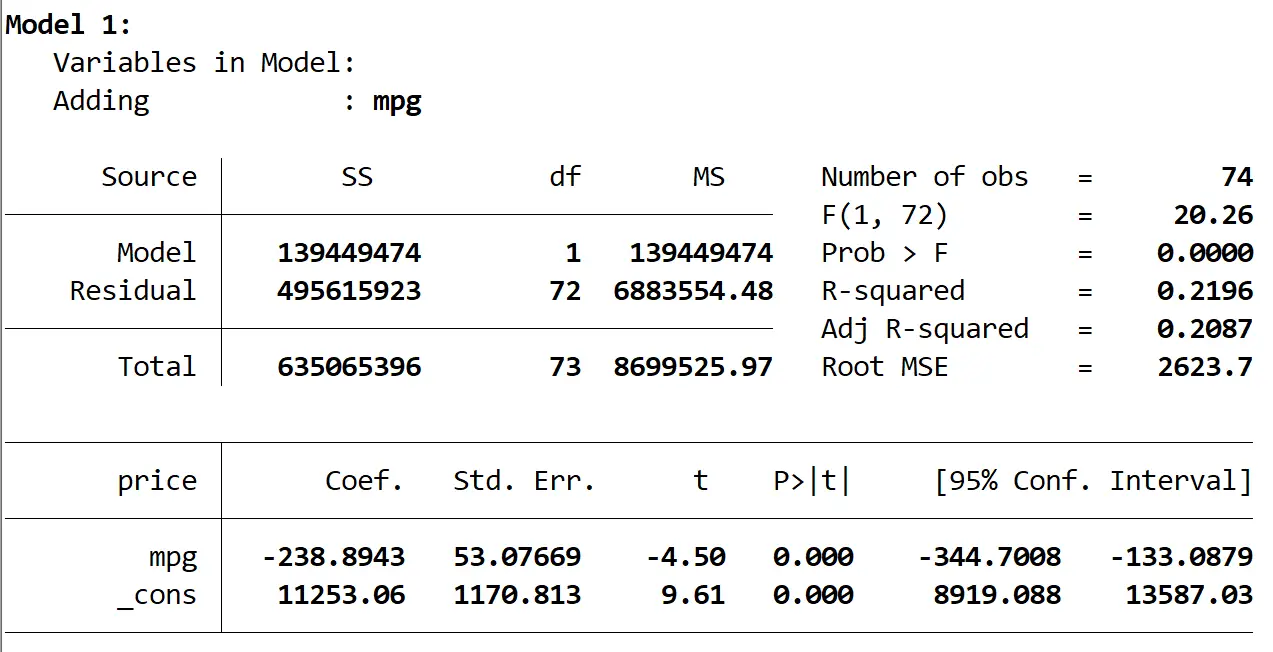
我们看到模型的 R 平方为0.2196 ，模型的总体 p 值 (Prob > F) 为0.0000 ，在 α = 0.05 时具有统计显着性。

接下来我们看第二个模型的结果：

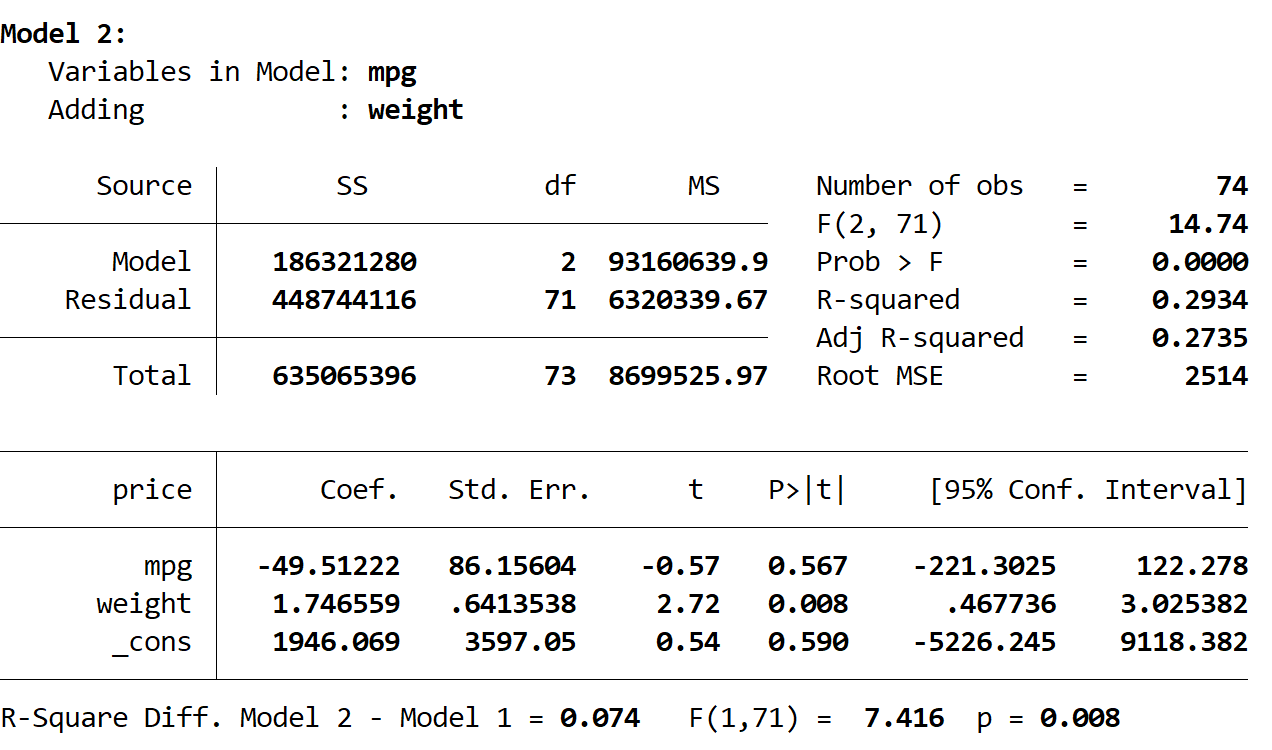
该模型的 R 方为0.2934 ，比第一个模型的 R 方大。为了确定这种差异是否具有统计显着性，Stata 进行了 F 检验，结果底部给出了以下数字：

• 两个模型之间的 R 平方差 = 0.074
• 差异 F 统计量 = 7.416
• F 统计量的相应 p 值 = 0.008

由于 p 值小于 0.05，我们得出结论，与第一个模型相比，第二个模型在统计上有显着的改进。

最后我们可以看到第三个模型的结果：

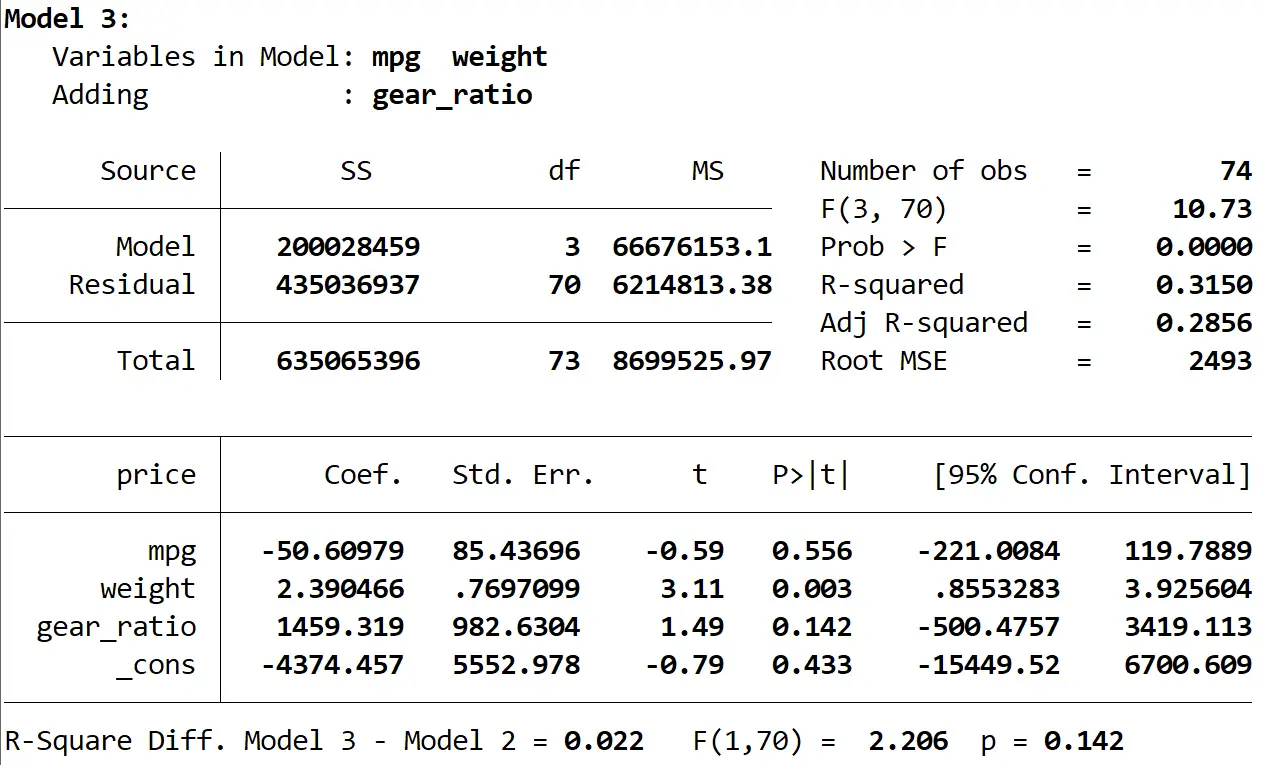
该模型的 R 方为0.3150 ，比第二个模型的 R 方大。为了确定这种差异是否具有统计显着性，Stata 进行了 F 检验，结果底部给出了以下数字：

• 两个模型之间的 R 平方差 = 0.022
• 差异 F 统计量 = 2.206
• F 统计量的相应 p 值 = 0.142

由于 p 值不小于 0.05，因此我们没有足够的证据表明第三个模型比第二个模型有所改进。

在结果的最后，我们可以看到Stata提供了结果摘要：

在这个特定示例中，我们得出的结论是，模型 2 比模型 1 提供了显着改进，但模型 3 并没有比模型 2 提供显着改进。