如何在 r 中执行嵌套方差分析（逐步）

嵌套方差分析是方差分析（“方差分析”）的一种，其中至少一个因素嵌套在另一个因素中。

例如，假设研究人员想知道三种不同的肥料是否会产生不同程度的植物生长。

为了测试这一点，三名不同的技术人员每人在四株植物上喷洒肥料 A，另外三名技术人员每人在四株植物上喷洒肥料 B，另外三名技术人员每人在四株植物上喷洒肥料 C。

在这种情况下，响应变量是植物生长，两个因素是技术人员和肥料。原来，技术员正窝在肥料里：

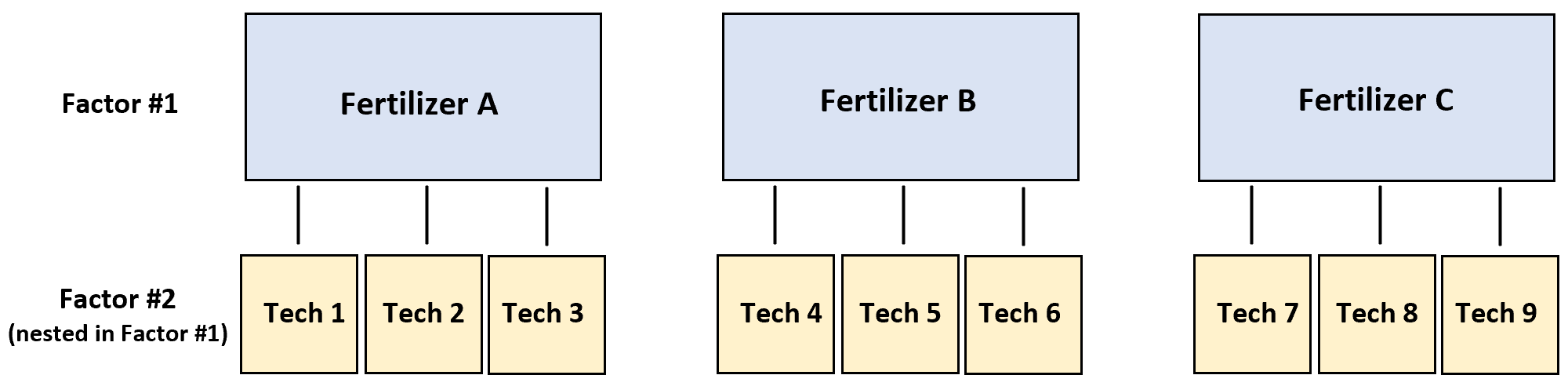
以下分步示例展示了如何在 R 中执行此嵌套方差分析。

第 1 步：创建数据

首先，让我们创建一个数据框来保存 R 中的数据：

 #create data
df <- data. frame (growth=c(13, 16, 16, 12, 15, 16, 19, 16, 15, 15, 12, 15,
                          19, 19, 20, 22, 23, 18, 16, 18, 19, 20, 21, 21,
                          21, 23, 24, 22, 25, 20, 20, 22, 24, 22, 25, 26),
                 fertilizer=c(rep(c(' A ', ' B ', ' C '), each= 12 )),
                 tech=c(rep(1:9, each= 4 )))

#view first six rows of data
head(df)

  growth fertilizer tech
1 13 A 1
2 16 A 1
3 16 A 1
4 12 A 1
5 15 A 2
6 16 A 2

第 2 步：调整嵌套方差分析

我们可以使用以下语法来拟合 R 中的嵌套方差分析：

aov（答案〜因素A /因素B）

金子：

• 响应：响应变量
• 因素A：第一个因素
• 因素 B：嵌套在第一个因素中的第二个因素

以下代码显示了如何为我们的数据集拟合嵌套方差分析：

 #fit nested ANOVA
nest <- aov(df$growth ~ df$fertilizer / factor(df$tech))

#view summary of nested ANOVA
summary(nest)

                              Df Sum Sq Mean Sq F value Pr(>F)    
df$fertilizer 2 372.7 186.33 53.238 4.27e-10 ***
df$fertilizer:factor(df$tech) 6 31.8 5.31 1.516 0.211    
Residuals 27 94.5 3.50                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

第 3 步：解释结果

我们可以查看 p 值列来确定每个因素是否对植物生长具有统计上显着的影响。

从上表中我们可以看出，肥料对植物生长具有统计显着性影响（p 值 < 0.05），但技术人员则没有（p 值 = 0.211）。

这告诉我们，如果我们想促进植物生长，我们需要关注所使用的肥料，而不是施用肥料的个别技术人员。

第 4 步：可视化结果

最后，我们可以使用箱线图来可视化按肥料和按技术人员划分的植物生长分布：

 #load ggplot2 data visualization package
library (ggplot2)

#create boxplots to visualize plant growth
ggplot(df, aes (x=factor(tech), y=growth, fill=fertilizer)) +
  geom_boxplot()

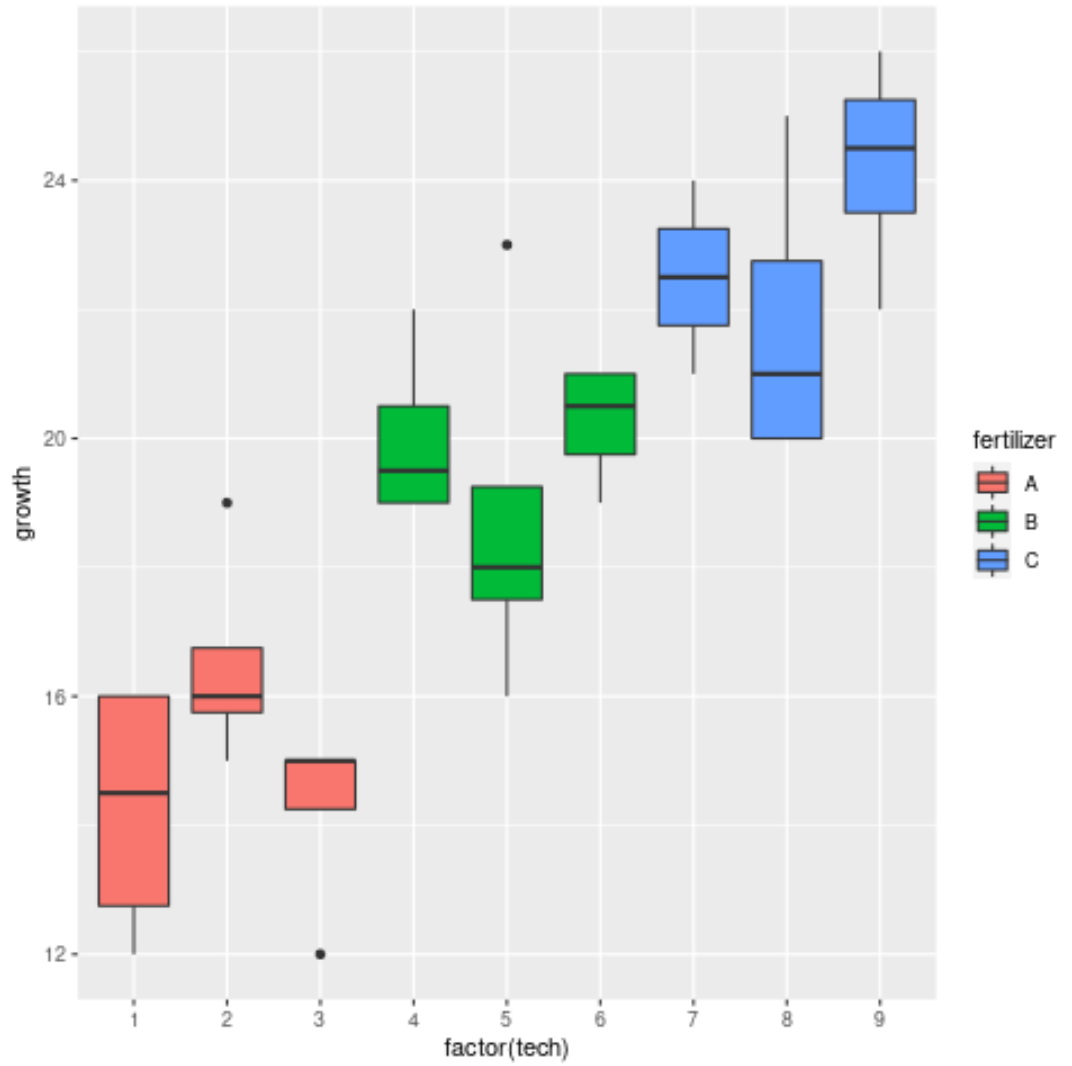
该图显示，三种不同肥料之间的生长存在显着差异，但每个肥料组内的技术人员之间的差异并不大。

这似乎与嵌套方差分析的结果相匹配，并证实肥料对植物生长有显着影响，但个别技术人员却没有。

其他资源

如何在 R 中执行单向方差分析
如何在 R 中执行双向方差分析
如何在 R 中执行重复测量方差分析