什么是嵌套方差分析？ （定义&#038；示例）

嵌套方差分析是方差分析（“方差分析”）的一种，其中至少一个因素嵌套在另一个因素中。

注意：有时嵌套方差分析称为“层次方差分析”。这两个术语经常互换使用。

例如，假设我们想知道三种不同的肥料是否会产生不同程度的植物生长。

为了测试这一点，三名不同的技术人员每人在四株植物上喷洒肥料 A，另外三名技术人员每人在四株植物上喷洒肥料 B，另外三名技术人员每人在四株植物上喷洒肥料 C。

在这种情况下，响应变量是植物生长，两个因素是技术人员和肥料。原来，技术员正窝在肥料里：

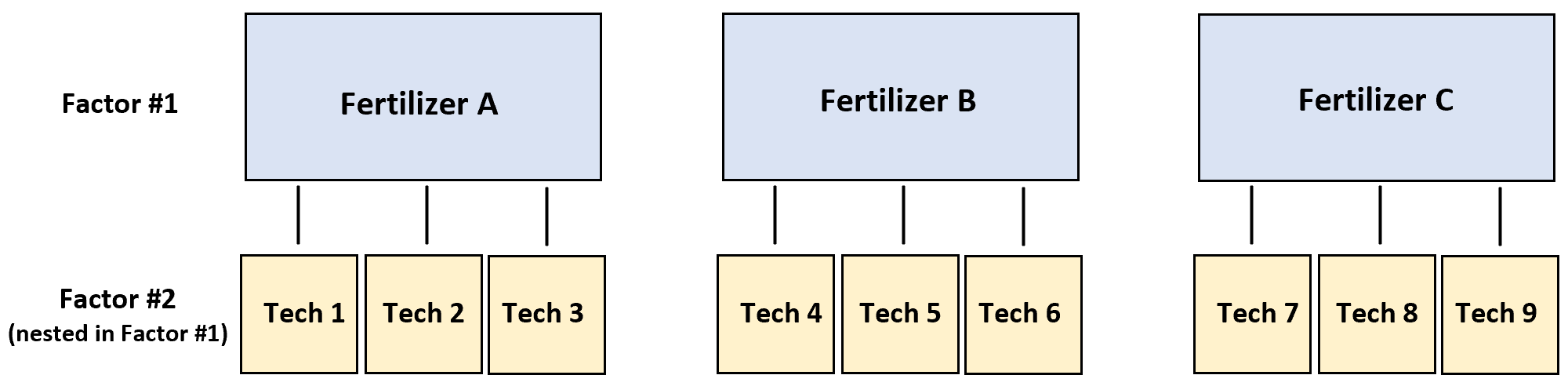
原始数据如下所示：

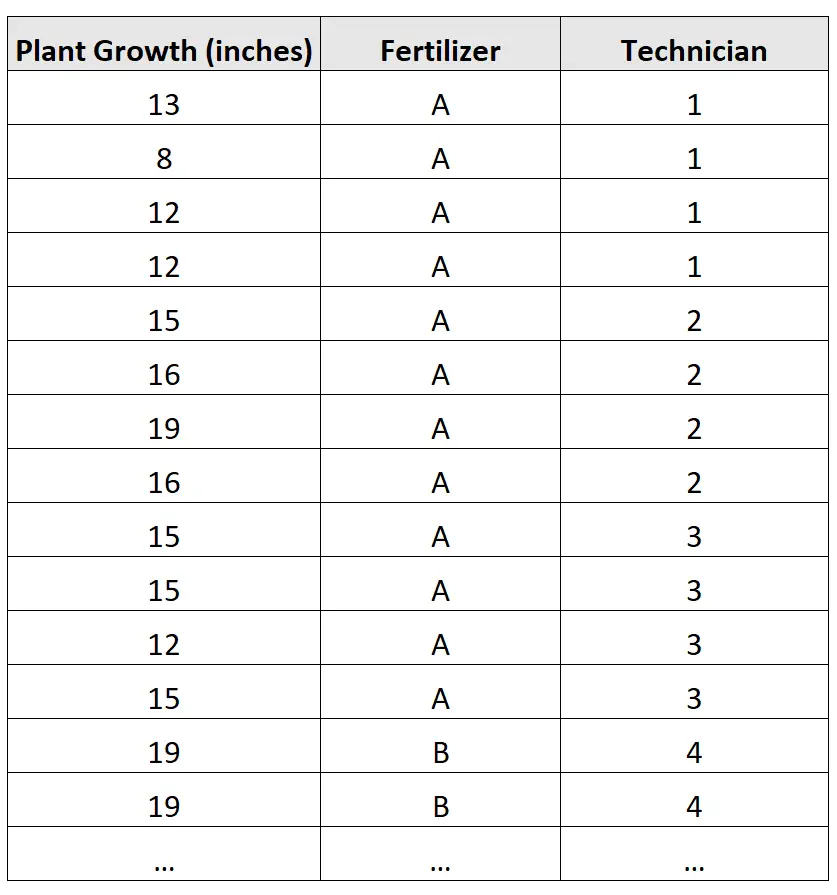
在这种情况下，嵌套方差分析可以测试两件事：

• 植物生长在因子 1（肥料）的各个水平上是否相同？
• 植物生长在因子 2 的每个水平上是否相等（技术人员）？

当我们进行嵌套方差分析（使用 R、Excel、SPSS 等统计软件）时，结果将采用以下格式：

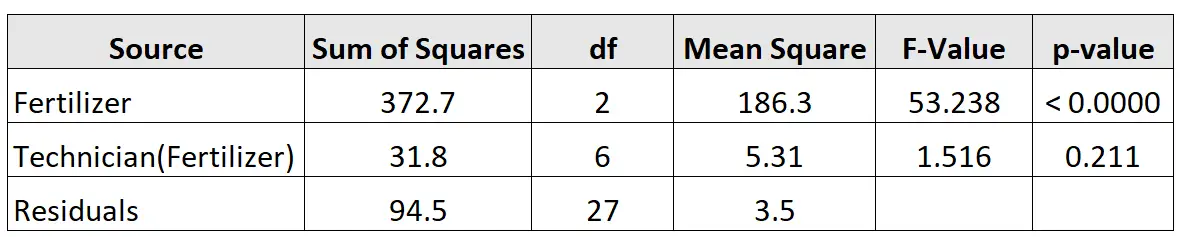
以下是如何解释结果：

• 来源：差距的来源
• 平方和：偏差平方和
• df：自由度
• 均方：均方，计算方式为平方和 / df
• F 值： F 值，计算为均方/均方残差
• p 值：对应于 F 值的 p 值

我们可以查看p 值列来确定每个因素是否对植物生长具有统计上显着的影响。

从上表中我们可以看出，肥料对植物生长具有统计显着性影响（p 值 < 0.05），但技术人员则没有（p 值 = 0.211）。

这告诉我们，如果我们想促进植物生长，我们需要关注所使用的肥料，而不是施用肥料的个别技术人员。

评论

以下是有关嵌套方差分析需要记住的一些注意事项：

1. 嵌套方差分析可以有两个以上的因素。

在前面的示例中，嵌套方差分析有两个因素，一个因素嵌套在另一个因素之内。但是，嵌套方差分析可以有两个以上相互嵌套的因素。

2. 嵌套方差分析与双向方差分析不同。

在嵌套方差分析中，至少一个因素嵌套在另一个因素内。这与双向方差分析不同，双向方差分析也有两个因素，但两个因素都不嵌套在另一个因素中。

例如，在前面的场景中，假设每个技术人员都施用每种类型的肥料。在这种情况下，我们可以执行双向方差分析，因为技术和肥料的所有可能组合都出现在数据集中。

如何在实践中执行嵌套方差分析

以下教程介绍了如何在 Excel 和 R 中执行嵌套方差分析：

• 如何在 R 中执行嵌套方差分析
• 如何在 Excel 中执行嵌套方差分析