工具变量：定义和示例

通常，在统计学中，我们试图估计一个变量对另一个变量的影响。例如，我们可能想知道：

• 学习时间如何影响考试成绩？
• 某种药物如何影响血压？
• 压力如何影响心率？

在每种情况下，我们都想了解预测变量是否影响响应变量。然而，通常还有其他变量影响两个变量之间的关系。

例如，假设我们使用某种药物作为预测变量，血压作为响应变量。我们只关心药物对血压的影响：

然而，其他变量，如锻炼时间、一般饮食和压力水平也会影响血压：

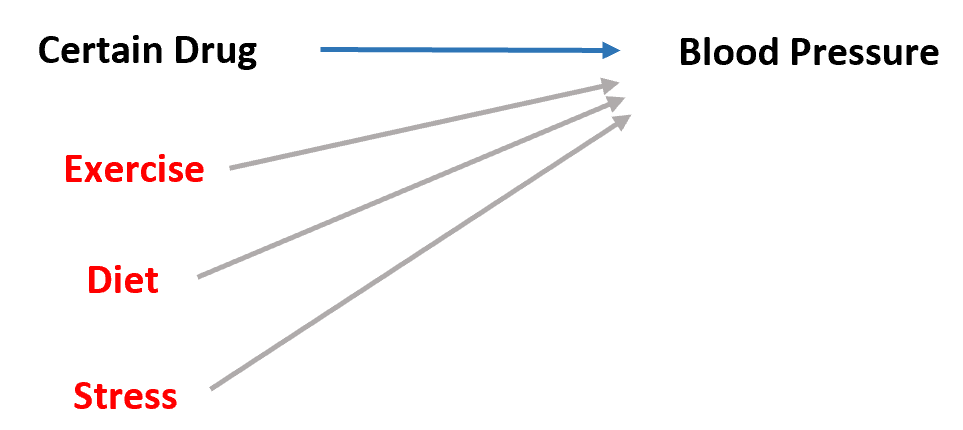
因此，如果我们使用药物作为预测变量、血压作为响应变量进行简单的线性回归，我们不能确定回归系数能否准确地捕捉药物对血压的影响，因为外部因素（运动、饮食、压力等）也可能发挥作用。

解决这个问题的一种可能的方法是使用工具变量。

什么是工具变量？

工具变量是引入回归分析的第三个变量，它与预测变量相关，但与响应变量不相关。使用此变量，可以估计预测变量对响应变量的真实因果效应。

例如，假设我们想要估计某种药物对血压的影响：

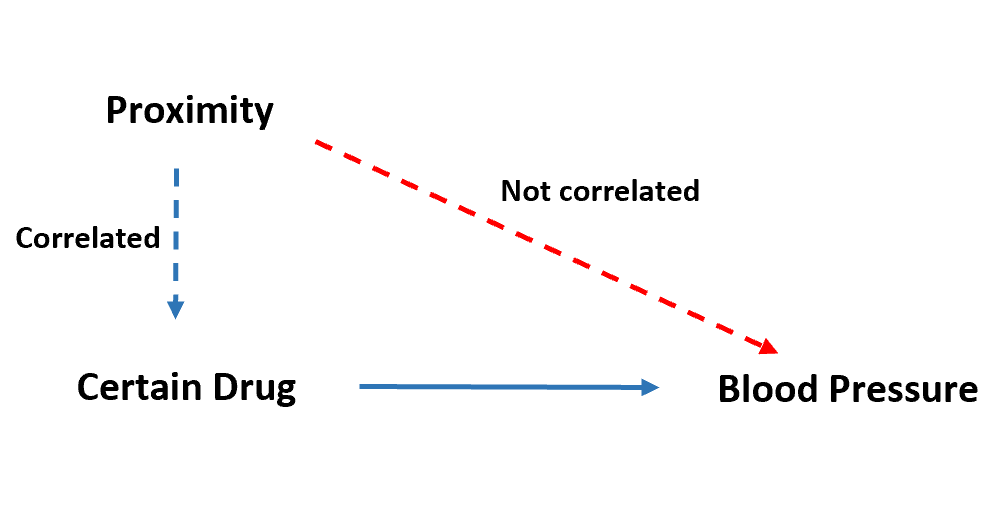
我们可以在此回归分析中使用的工具变量的一个示例是个人与药房的接近程度。

这种“邻近”变量可能与个人是否服用相关药物高度相关，因为如果个人不住在药房附近，他们首先就无法获得该药物。

然而，“邻近”变量不应与血压有任何相关性。它与血压的唯一关联是通过预测变量。

我们实际使用工具变量的方式是执行工具变量回归，有时称为两阶段最小二乘回归。

工具变量回归

工具变量回归（或两阶段最小二乘回归）使用以下方法来估计预测变量对响应变量的影响：

步骤 1：使用工具变量作为预测变量拟合回归模型。

在我们的具体示例中，我们首先拟合以下回归模型：

某些药物 = B ₀ + B ₁ （接近）

然后，我们将得到某些药物 (cd) 的预测值，我们将其称为 cd _hat 。

步骤 2：使用 cd _hat的预测值拟合第二个回归模型。

接下来，我们将拟合以下回归模型：

血压 = B ₀ + B ₁ (cd _hat )

如果发现cd _hat的回归系数具有统计显着性，那么我们可以说该药物对血压存在因果作用。

我们之所以可以这样说，是因为我们只使用“邻近度”这个术语来创建 CD _Hat ，并且我们知道邻近度不应该与血压相关，第二阶段回归中的任何显着相关性都可能归因于某种药物。

使用工具变量的注意事项

仅当工具变量满足以下条件时才应使用：

• 它与预测变量密切相关。
• 它与响应变量不相关。
• 它与模型中排除的其他变量不相关（例如，接近度与运动、饮食或压力不相关）。

如果工具变量不满足此标准，则不应在回归模型中使用它，因为它可能会产生不可靠且有偏差的结果。