Bartlett 方差齐性检验(定义和示例)
Bartlett 检验是一种统计检验,用于确定多个组之间的方差是否相等。
许多统计检验(例如单向方差分析)假设样本之间的方差相等。 Bartlett 检验可用于验证这一假设。
以下步骤说明如何执行 Bartlett 测试。
注意:请勿将此检验与Bartlett 球形度检验混淆,后者用于将观察到的相关矩阵与单位矩阵进行比较。
执行巴特利特测试的步骤
Bartlett 检验使用以下原假设和备择假设:
H 0 :各组之间的方差相等。
H A :至少一组的方差不等于其他组。
检验统计量可以计算如下:
B = (nk)lns 2 – Σ(n j -1)lns j 2 / c
金子:
- n:所有组中的观察总数
- k:组总数
- ln:这意味着“自然对数”
- s 2 :合并方差
- n j :第 j 组中的观测值数量
- s j 2 :组 j 的方差
其计算方式如下:
- c = 1 + (1/3(k-1))*(Σ(1/(n j -1)) – (1/(nk))
该检验统计量遵循自由度为 k-1 的卡方分布。换句话说,B~X 2 (k-1)。
如果与检验统计量相对应的p 值低于一定的显着性水平(例如 α = 0.05),那么我们可以拒绝原假设并得出结论:并非所有组都具有相同的方差。
示例:巴特利特测试
假设一位教授想知道三种不同的学习技巧是否会导致考试的平均成绩不同。
她随机分配 10 名学生使用每种技术一周,然后为每个学生提供同等难度的考试。
30名同学的考试成绩如下:

教授想要执行单向方差分析,看看这三种技术是否会导致考试的平均分数不同,但她必须首先执行 Bartlett 检验,以验证三组的方差是否相等。
手动进行 Bartlett 检验比较繁琐,因此我们将以下数据值输入到Bartlett 检验计算器中:
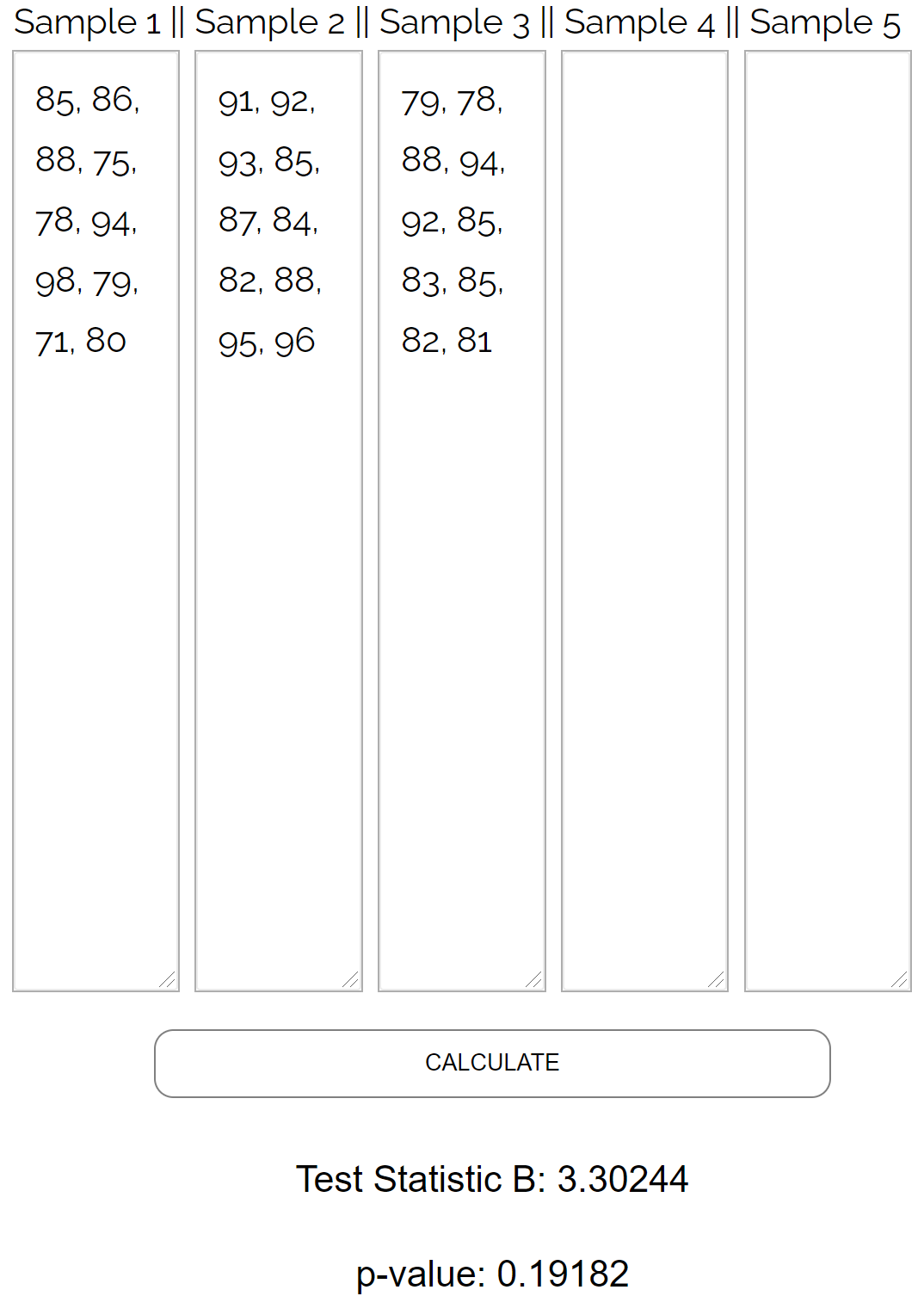
测试返回以下结果:
- 检验统计量B : 3.30244
- P 值: 0.19182
由于 p 值不小于 0.05,教授将无法拒绝原假设。换句话说,她没有足够的证据表明这三个群体有不同的差距。
因此,她可以继续进行单向方差分析。