如何在 stata 中执行 breusch-pagan 检验

多元线性回归是一种我们可以用来理解多个解释变量和响应变量之间关系的方法。

不幸的是，回归中经常出现的一个问题被称为异方差，其中残差的方差在一系列测量值上存在系统性变化。

我们可以用来确定是否存在异方差的一项测试是Breusch-Pagan 测试。该检验生成卡方检验统计量和相应的 p 值。

如果 p 值低于某个阈值（常见选择为 0.01、0.05 和 0.10），则有足够的证据表明存在异方差性。

本教程介绍如何在 Stata 中执行 Breusch-Pagan 检验。

示例：Stata 中的 Breusch-Pagan 检验

我们将使用自动集成的 Stata 数据集来说明如何执行 Breusch-Pagan 测试。

步骤1：加载并显示数据。

首先，使用以下命令加载数据：

系统自动使用

然后使用以下命令显示原始数据：

br

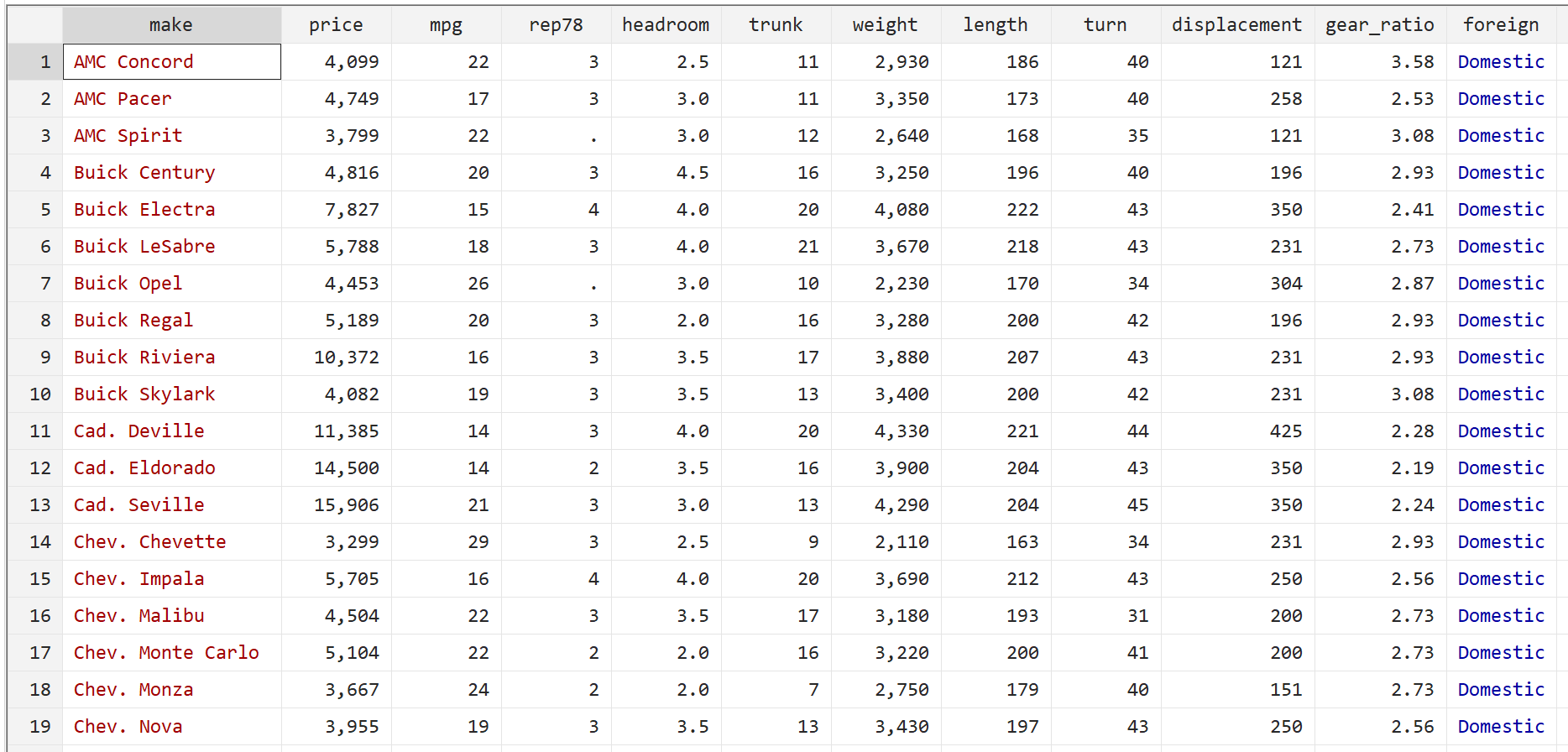
步骤 2：执行多元线性回归。

接下来，我们将输入以下命令来执行多元线性回归，使用价格作为响应变量， mpg和体重作为解释变量：

回归价格 mpg 重量

步骤 3：执行 Breusch-Pagan 测试。

一旦我们拟合了回归模型，我们就可以使用hettest命令执行 Breusch-Pagan 检验，该命令是“异方差检验”的缩写：

最热的

以下是如何解释结果：

Ho：这是检验的原假设，表明残差之间存在恒定方差。

变量：这告诉我们回归模型中使用的响应变量。在这种情况下，它是可变价格。

chi2(1)：这是检验的卡方检验统计量。在本例中，时间是下午 2:78。

Prob > chi2：这是对应于卡方检验统计量的 p 值。在本例中为 0.0001。该值小于 0.05，我们可以拒绝原假设并得出数据存在异方差的结论。

接下来做什么

如果您未能拒绝 Breusch-Pagan 检验的原假设，则不存在异方差，您可以继续解释原始回归的结果。

但是，如果拒绝 Breusch-Pagan 检验的原假设，则意味着数据中存在异方差性。在这种情况下，回归输出表中显示的标准误差是不可靠的。有多种方法可以解决此问题，包括：

1. 变换响应变量。您可以尝试对响应变量执行转换。例如，您可以使用 log(price) 而不是 Price 作为响应变量。一般来说，对响应变量取对数是消除异方差的有效方法。另一种常见的转换是使用响应变量的平方根。

2. 使用加权回归。这种类型的回归根据拟合值的方差为每个数据点分配权重。本质上，这为具有较高方差的数据点赋予了较低的权重，从而减少了它们的残差平方。当使用适当的权重时，可以消除异方差问题。

3. 使用稳健的标准误。稳健标准误差对于异方差问题更加“稳健”，并且往往能够更准确地测量回归系数的真实标准误差。查看本教程，了解如何在 Stata 回归中使用稳健的标准误差。