恒定方差假设：定义和示例

线性回归是一种用于量化一个或多个预测变量与响应变量之间关系的技术。

线性回归的关键假设之一是残差在预测变量的每个水平上具有恒定方差。

如果这个假设没有得到验证，残差将会受到异方差的影响。当这种情况发生时，模型系数估计变得不可靠。

如何评估常数方差

确定回归模型的残差是否具有恒定方差的最常见方法是创建拟合值相对于残差的图。

这是一种图，显示回归模型沿 x 轴的拟合值以及沿 y 轴拟合的这些值的残差。

如果残差分布在拟合值的每个水平上近似相等，我们就说满足常方差假设。

否则，如果残差的离散度系统性地增加或减少，则可能违反该假设。

注意：这种类型的图只能在将回归模型拟合到数据集后才能创建。

下图显示了显示常数方差的拟合值与残差的图示例：

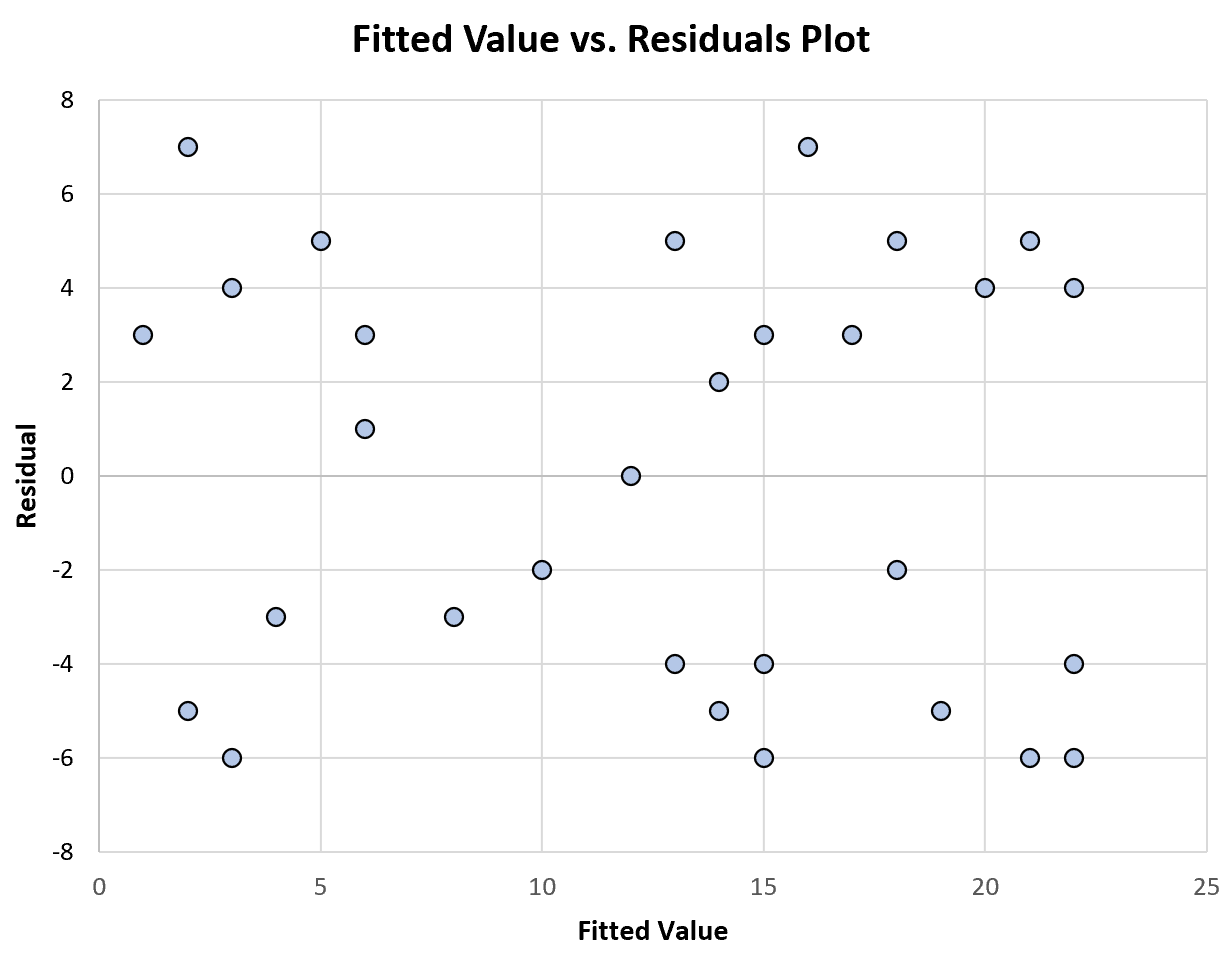
请注意残差如何随机分散在零附近，没有特定的模式，在拟合值的每个级别上方差近似恒定。

下图显示了显示非常量方差的拟合值与残差的图示例：

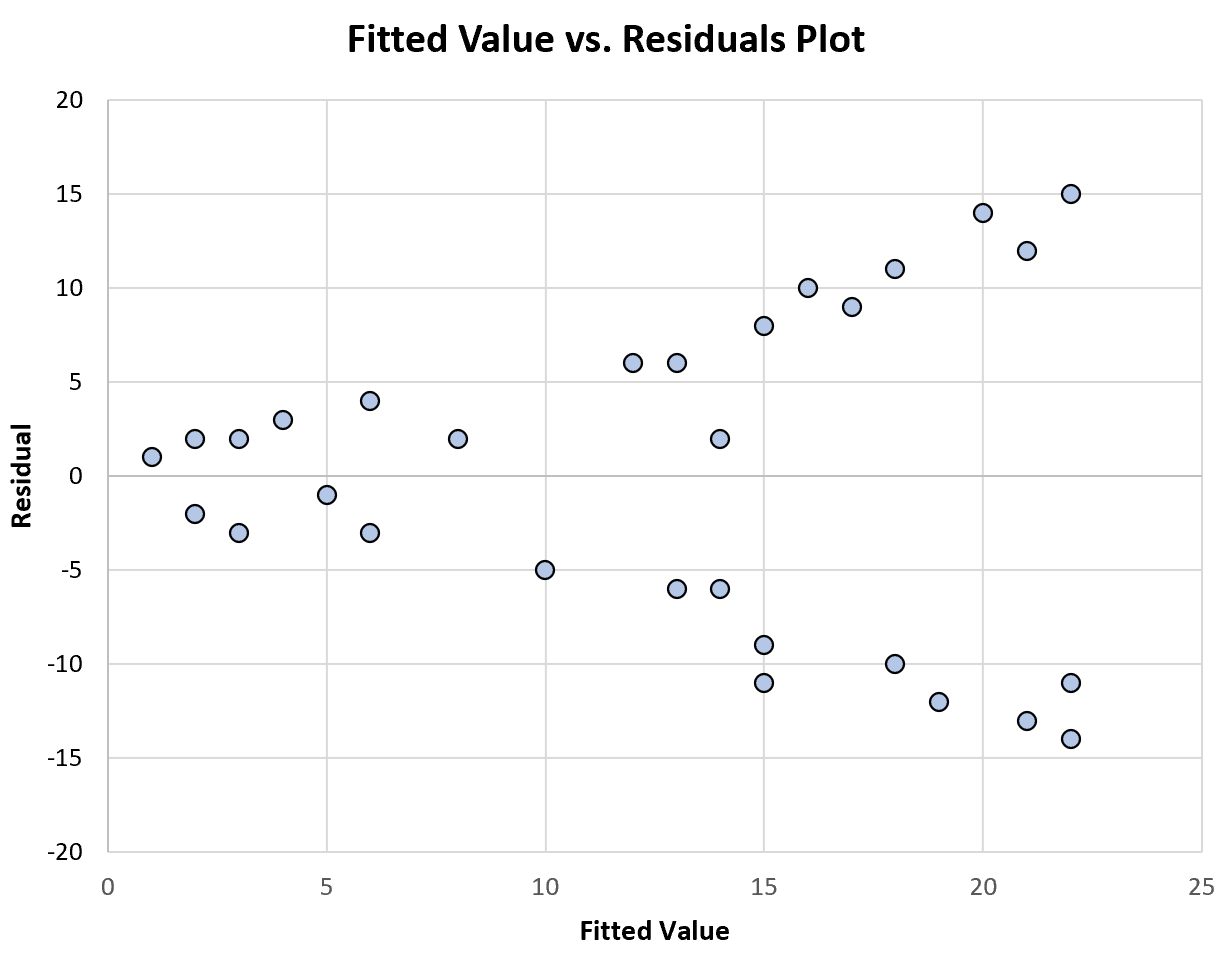
请注意，随着拟合值的增加，残差的分布变得更大。这是非恒定方差的典型标志。

这告诉我们，我们的回归模型的残差存在非恒定方差，因此模型系数估计是不可靠的。

如何解决常量方差违规问题

如果违反了恒定方差的假设，解决此问题的最常见方法是使用以下三种变换之一来变换响应变量：

1. Log变换：将响应变量从y变换为log(y)

2. 平方根变换：将响应变量从y变换为√y

3.立方根变换：将响应变量从y变换为y ^1/3

通过执行这些变换，非恒定方差的问题通常会消失。

其他资源

以下教程提供有关线性回归和残差分析的其他信息：

简单线性回归简介
多元线性回归简介
线性回归的四个假设
统计中的残差是什么？