为什么平均值在统计中很重要？

数据集的均值表示该数据集的平均值。计算方法如下：

平均值 = Σx _i / n

金子：

• Σ：表示“和”的符号
• x _i ：数据集中的第 i^个观察值
• n：数据集中的观测总数

例如，假设我们有以下包含 11 个观测值的数据集：

数据集： 3、4、4、6、7、8、12、13、15、16、17

数据集的平均值计算如下：

平均值 = (3+4+4+6+7+8+12+13+15+16+17) / 11 = 9.54

在统计学中，平均值很重要，原因如下：

1.平均值让我们了解数据集的“中心”在哪里。

2.由于其计算方式，平均值包含数据集中每个观测值的信息。

下面的例子说明了这两个原因。

示例：计算一组数据的平均值

假设我们有一个数据集，其中包含某个城市 10,000 套不同房屋的销售价格。

我们不需要查看数千行原始数据，而是可以计算平均值来快速了解该城市房屋的平均销售价格。

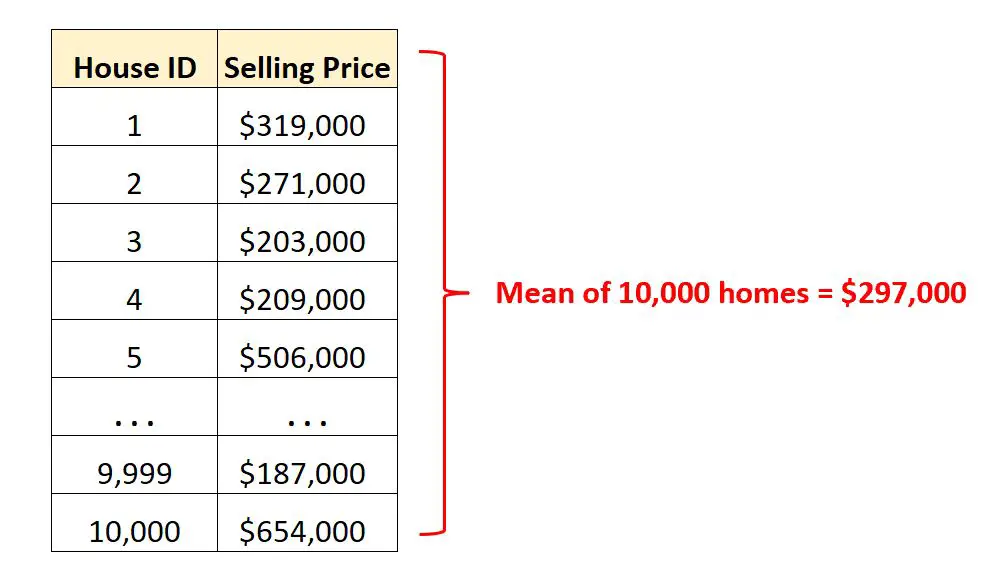
了解平均售价为 297,000 美元，让我们了解这座城市“典型”房屋的售价。

这个平均值的单个值比查看所有原始数据行更容易解释。

由于每栋房屋的销售价格都用于计算平均值，因此我们可以将平均销售价格乘以房屋总数，得出该城市所有房屋的总销售价格：

• 所有房屋的总销售价格 = 平均销售价格 * 房屋数量
• 所有房屋的总销售价格 = $297,000 * 10,000
• 所有房屋的总销售价格 = $2,970,000,000

我们可以看到这个城市所有房屋的总销售价格是29.7亿美元。

何时使用平均值

在分析数据集时，我们常常想了解中心价值在哪里。

在统计学中，我们使用两个常见的指标来衡量数据集的中心：

• 平均值：一组数据的平均值
• 中位数：数据集中的中值

平均值是衡量数据集中心的最常见方法，但在以下情况下它实际上可能会产生误导：

• 当分布不对称时。
• 当分布包含异常值时。

为了说明这一点，请考虑以下两个示例。

示例 1：计算偏态分布的平均值

考虑某个城市居民的工资分布如下：

分布右侧的高工资使平均值远离分布的中心。

因此，中位数比平均值更好地反映了居民的“典型”工资，因为分布向右倾斜。

在此特定示例中，平均工资为 47,000 美元，而中位数工资为 32,000 美元。

因此，中位数更能代表该城市的典型工资。

示例 2：计算存在异常值的情况下的平均值

考虑下图，它显示了某条街道上房屋的平方英尺：

平均值很大程度上受到一些非常大的房屋的影响，而中位数则不然。

我们可以看到，中位数比平均值更能捕捉该街道上房屋的“典型”平方英尺，因为它不受异常值的影响。

概括

以下是本文主要内容的简要总结：

• 平均值表示一组数据的平均值。
• 平均值很重要，因为它让我们了解数据集中的中心值在哪里。
• 平均值也很重要，因为它包含数据集中每个观察值的信息。
• 当数据集有偏差或包含异常值时，平均值可能会产生误导。在这些情况下，中位数可以更精确地了解数据集的“中心”在哪里。

其他资源

以下教程提供了有关其他描述性统计的附加信息：

为什么中位数在统计学中很重要？
为什么标准差在统计学中很重要？
何时使用均值与中位数