如何求多个标准差的平均值

有时您可能想要找到两个或多个标准差的平均值。

为此，您可以根据您的数据使用以下两个公式之一：

方法一：等样本量

如果要求k组之间的平均标准差，并且每组具有相同的样本量，可以使用以下公式：

平均 SD = √ (s ₁ ² + s ₂ ² + … + s _k ² ) / k

金子：

• _sk ：^{第 k}组的标准差
• k : 组总数

方法 2：样本量不等

如果要求k组之间的平均标准差，并且每组的样本量不相同，可以使用以下公式：

平均值 SD = √ ((n ₁ -1)s ₁ ² + (n ₂ -1)s ₂ ² + … + (n _k -1)s _k ² ) / (n ₁ +n ₂ + … + n _k – j)

金子：

• n _k ：第^k组的样本大小
• _sk ：^{第 k}组的标准差
• k : 组总数

以下示例展示了如何在实践中使用每个公式。

方法 1：计算相同样本量的标准差平均值

假设我们要计算以下六个销售周期内销售额的平均标准差：

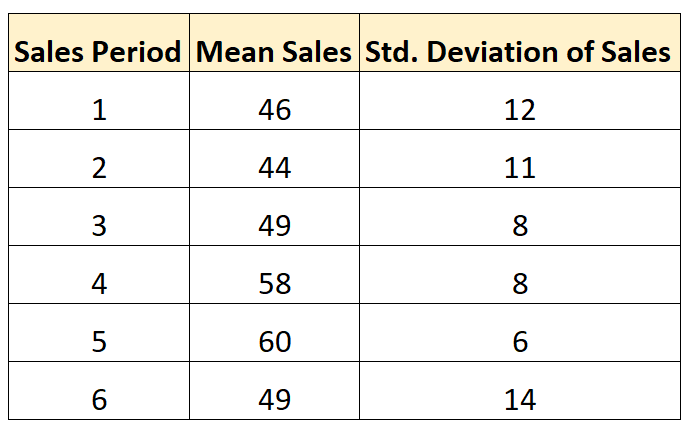
假设我们在每个销售期间进行了相同数量的销售交易。我们可以使用以下公式来计算每个时期销售额的平均标准差：

• 平均标准差 = √ (s ₁ ² + s ₂ ² + … + s _k ² ) / k
• 平均标准差 = √ (12 ² + 11 ² + 8 ² + 8 ² + 6 ² + 14 ² ) / 6
• 平均标准差 = 10.21

每期销售额的平均标准差为10.21 。

方法 2：对不同样本量的标准差进行平均

假设我们要计算以下六个销售周期内销售额的平均标准差：

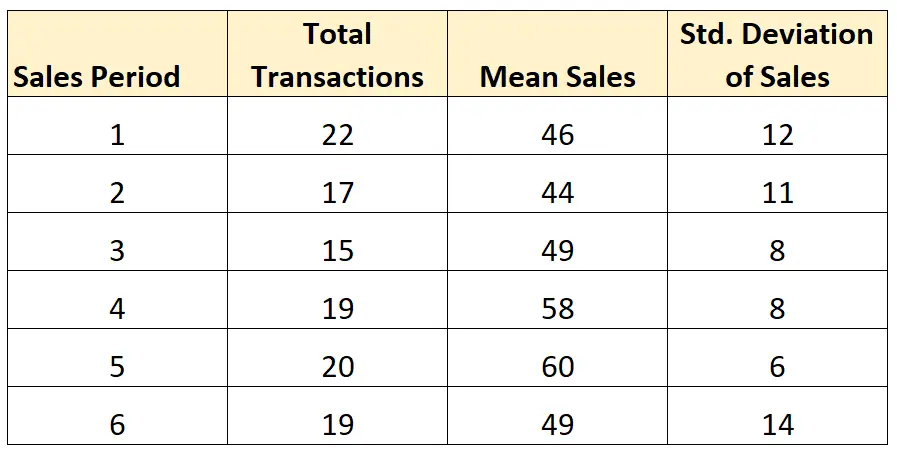
由于每个销售期间的样本量（总交易量）并不相等，因此我们将使用以下公式计算每个期间销售的平均标准差：

• 平均值 SD = √ ((n ₁ -1)s ₁ ² + (n ₂ -1)s ₂ ² + … + (n _k -1)s _k ² ) / (n ₁ +n ₂ + … + n _k – j)
• 平均SD = √ ((21)12 ² + (16)11 ² + (14)8 ² + (18)8 ² + (19)6 ² + (18)14 ² ) / 106
• 平均标准差 = 10.29

每期销售额的平均标准差为10.29 。

请注意，两个示例中的平均标准差非常相似。这是因为第二个示例中的样本大小（总交易量）彼此非常接近。

仅当组间样本量显着不同时，两种计算平均标准差的方法才会显着不同。