什么是平衡精度？ （定义&；示例）
平衡准确度是我们可以用来评估分类模型性能的一个指标。
计算方法如下：
平衡准确度= (灵敏度 + 特异性) / 2
金子：
- 灵敏度：“真阳性率”——模型能够检测到的阳性病例的百分比。
- 特异性：“真阴性率”——模型能够检测到的阴性病例的百分比。
当两个类不平衡时，即一个类出现的次数比另一类多得多时，该指标特别有用。
以下示例展示了如何在实践中计算平衡准确性，并说明了为什么它是一个如此有用的指标。
示例：计算平衡精度
假设体育分析师使用逻辑回归模型来预测 400 名不同的大学篮球运动员是否会被选入 NBA。
以下混淆矩阵总结了模型所做的预测：
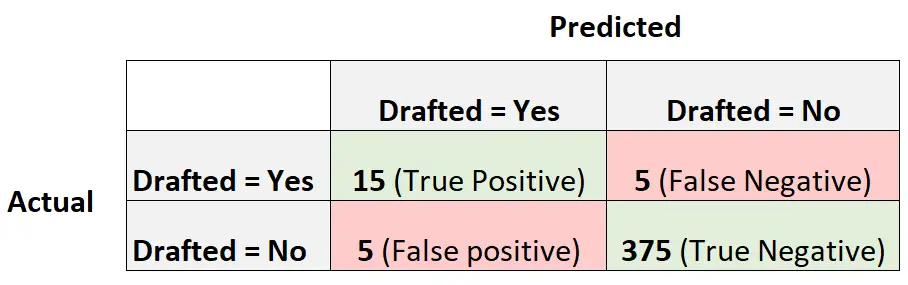
为了计算模型的平衡精度，我们首先计算灵敏度和特异性：
- 灵敏度：“真阳性率”= 15 / (15 + 5) = 0.75
- 特异性：“真阴性率”= 375 / (375 + 5) = 0.9868
然后我们可以计算平衡精度如下：
- 平衡准确度 = (灵敏度 + 特异性) / 2
- 平衡精度 = (0.75 + 9868) / 2
- 平衡精度 = 0.8684
模型的平衡精度为0.8684 。
请注意，平衡精度越接近 1，模型就越能够正确地对观测值进行分类。
在这个例子中，平衡精度相当高，这告诉我们逻辑回归模型在预测大学球员是否会被选入 NBA 方面做得非常好。
在这种情况下，由于类别非常不平衡（20 名球员被征召入伍，380 名球员没有被征召），与整体准确度测量相比，平衡准确度为我们提供了更真实的模型性能图景。
例如，我们将按如下方式计算模型精度：
- 准确度 = (TP + TN) / (TP + TN + FP + FN)
- 准确度 = (15 + 375) / (15 + 375 + 5 + 5)
- 准确度 = 0.975
该模型的准确度为0.975 ，看起来非常高。
然而，考虑一个简单预测每个球员都会落选的模型。其精度为 380/400 = 0.95 。这仅略低于我们模型的准确性。
0.8684的平衡准确度分数让我们更好地了解模型预测这两个类别的能力。
换句话说，它让我们更好地了解模型预测哪些球员会落选以及哪些球员会落选的能力。
其他资源
以下教程解释了如何在不同的统计软件中创建混淆矩阵：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多