什么是并行形式可靠性？ （定义&#038；示例）

在统计学中，并行形式可靠性衡量测试的两个等效形式之间的相关性。

并行形式的可靠性计算过程如下：

步骤 1：将测试分成两半。

例如，将 100 个问题的测试随机分为包含 50 个问题的测试 A 和也包含 50 个问题的测试 B。

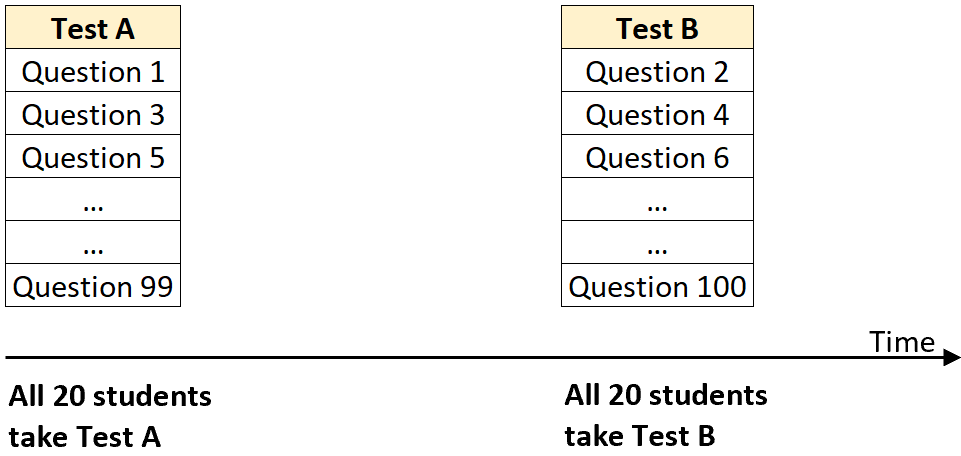
步骤 2：对所有学生进行前半部分，然后对所有学生进行后半部分。

例如，对某个班级的所有 20 名学生进行测试 A 并记录他们的分数。然后，也许一个月后，对同样的 20 名学生进行测试 B，并记录他们在该测试中的分数。

步骤3：计算两次测试的测试分数之间的相关性。

计算两次测试分数之间的相关性。如果分数之间的相关性很高，则称测试具有平行形式可靠性。

何时使用并行形式可靠性

当教授不希望学生提前获得测试问题时，通常在学术环境中使用并行形式可靠性。

例如，如果教授在学期开始时向所有学生分发测试A，然后在学期结束时分发相同的测试A，学生只需记住第一次测试的问题和答案即可。

然而，通过在学期结束时进行不同的 B 测试（希望难度相同），教授能够评估学生的知识，同时确保学生以前没有见过这些问题。

并行形式可靠性的潜在缺点

并行形式的可靠性有两个潜在的缺点：

1.需要提出很多问题。

并行形式可靠性最适合包含大量问题（例如 100 个问题）的测试，因为我们计算的相关性数量会更可靠。

2. 不能保证两半实际上是平行的。

当我们将测试随机分为两半时，并不能保证这两半的难度实际上是平行的或“相等”的。这意味着两项测试的分数可能会有所不同，仅仅是因为其中一半比另一项更难。

并行形式可靠性和分半可靠性

并行形式可靠性与减半可靠性类似，但略有不同：

可靠性分为两部分：

这涉及将测试分为两半，并将每一半对同一组学生进行。学生参加考试的顺序并不重要。

这种方法的优点是可以衡量内部一致性。理想情况下，我们希望两半之间的相关性较高，因为这表明测试的所有部分对所测量的内容都有同等的贡献。

并行形式的可靠性：

这涉及将测试分为两半（称为“A”和“B”），并将每一半测试给同一组学生。

然而，重要的是所有学生首先参加“A”测试，然后参加“B”测试，因此知道“A”测试的答案并不会给后来参加“A”测试的学生带来任何好处。 B”。

其他资源

可靠性分析快速介绍
什么是可靠性一分为二？
什么是重测信度？
什么是评估者间的可靠性？