Breusch-pagan 测试:定义和示例
线性回归的关键假设之一是残差在预测变量的每个水平上以相等方差分布。这种假设称为同方差性。
当不遵守此假设时,残差中就存在异方差性。当这种情况发生时,回归结果变得不可靠。
直观地检测是否存在异方差的一种方法是创建残差与回归模型拟合值的关系图。
如果图中残差在较高值处分布得更广,则表明存在异方差性。
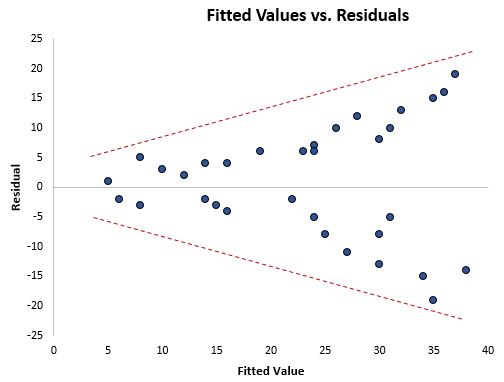
我们可以用来确定异方差是否存在的正式统计检验是Breusch-Pagan 检验。
本教程提供了 Breusch-Pagan 测试的简要说明以及示例。
什么是布洛伊施-异教测试?
Breusch-Pagan 检验用于确定回归模型中是否存在异方差。
该检验使用以下原假设和备择假设:
- 零假设 (H 0 ):存在同方差性(残差以等方差分布)
- 备择假设 ( HA ):存在异方差性(残差不以等方差分布)
如果检验的 p 值低于一定的显着性水平(即 α = 0.05),则我们拒绝原假设并得出回归模型中存在异方差的结论。
我们使用以下步骤来执行 Breusch-Pagan 测试:
1.拟合回归模型。
2.计算模型残差的平方。
3.使用残差的平方作为响应值,拟合新的回归模型。
4.以 n*R 2 new 的形式计算卡方 X 2检验统计量,其中:
- n:观察总数
- R 2 new :新回归模型的 R 平方,使用残差的平方作为响应值
如果与具有p (预测变量的数量)自由度的卡方检验统计量对应的 p 值低于一定的显着性水平(即 α = 0.05),则拒绝原假设并得出异方差存在的结论。
否则,不要拒绝原假设。在这种情况下,假设存在同方差性。
请注意,大多数统计软件都可以轻松执行 Breusch-Pagan 测试,因此您可能永远不需要手动执行这些步骤,但了解幕后发生的情况会很有帮助。
Breusch-Pagan 测试的一个例子
假设我们有以下数据集,其中包含 10 名不同篮球运动员的信息:
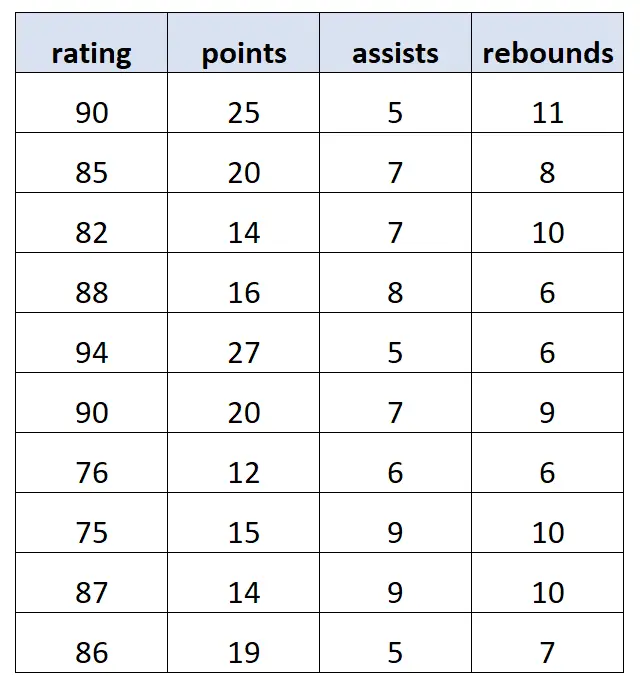
使用统计软件,我们拟合以下多元线性回归模型:
得分 = 62.47 + 1.12*(得分) + 0.88*(助攻) – 0.43*(篮板)
然后,我们使用该模型对每个玩家的评分进行预测并计算残差平方(即预测评分与实际评分之间的平方差):
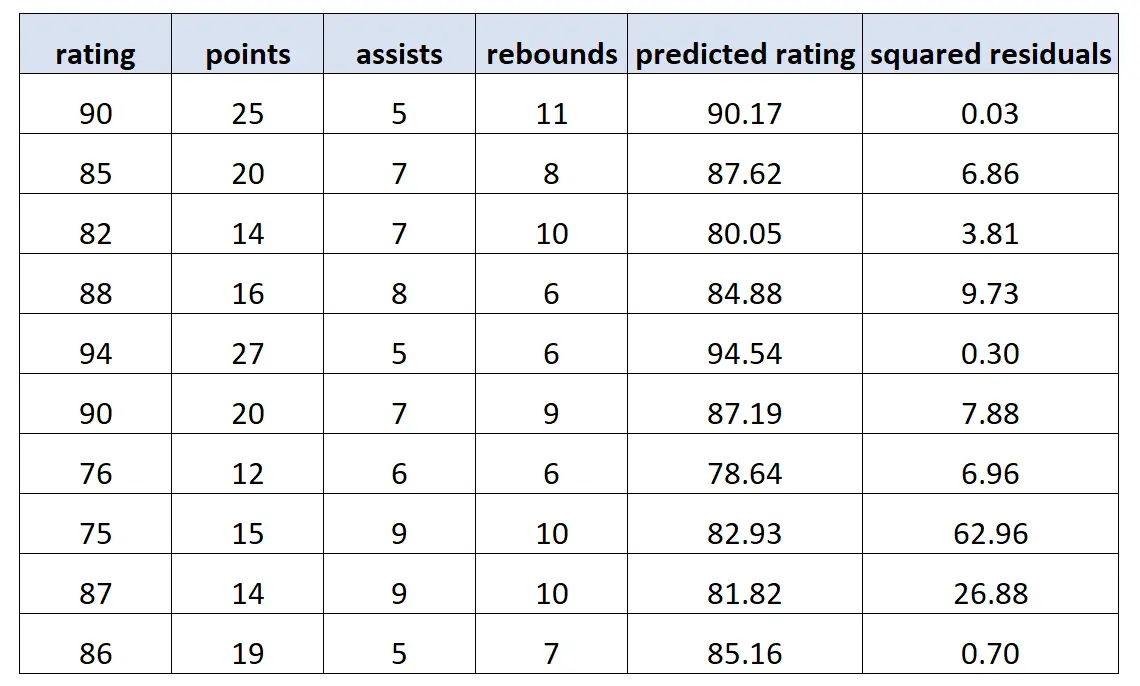
接下来,我们再次使用残差的平方作为响应值和原始预测变量作为预测变量来拟合新的回归模型。我们发现以下内容:
- 数量: 10
- R 2新: 0.600395
因此,我们的 Breusch-Pagan 检验的卡方检验统计量为 n*R 2 new = 10*.600395 = 6.00395 。自由度为p = 3 个预测变量。
根据卡方P值计算器,3个自由度的X 2 = 6.00395对应的p值为0.111418 。
由于该 p 值不小于 0.05,因此我们无法拒绝原假设。因此,我们假设存在同方差性。
实践中的布劳施-异教徒测试
以下教程提供了有关如何在不同统计程序中执行 Breusch-Pagan 检验的分步示例:
如何在 Excel 中执行 Breusch-Pagan 检验
如何在 R 中执行 Breusch-Pagan 测试
如何在 Python 中执行 Breusch-Pagan 测试
如何在 Stata 中执行 Breusch-Pagan 检验