如何手动执行卡方检验（逐步）

卡方拟合优度检验用于确定分类变量是否遵循假设分布。

以下分步示例演示如何手动执行卡方拟合优度检验。

手动卡方拟合优度检验

假设我们相信某个骰子是正确的。换句话说，我们相信在给定的掷骰中，骰子落在 1、2、3、4、5 或 6 上的概率相同。

为了测试这一点，我们将它扔了 60 次并记录它每次落地的数字。结果如下：

• 1 ：8次
• 2：12次
• 3：18次
• 4 ：9次
• 5 :7次
• 6 ：6次

按照以下步骤执行卡方拟合优度检验以确定骰子是否公平。

步骤 1：定义原假设和备择假设

• H ₀ （空）：骰子落在每个数字上的概率相同。
• H ₁ （替代）：骰子落在每个数字上的概率不同。

第 2 步：计算观察到的频率和预期频率

接下来，让我们为骰子上的每个数字创建一个观察到的频率和预期的频率表：

注意：如果我们认为骰子是公平的，这意味着我们期望骰子落在每个数字上的次数相同 – 在本例中，每个数字 10 次。

步骤 3：计算检验统计量

卡方检验统计量 X ²计算如下：

• X ² = Σ(OE) ² / E

下表显示了如何计算此检验统计量：

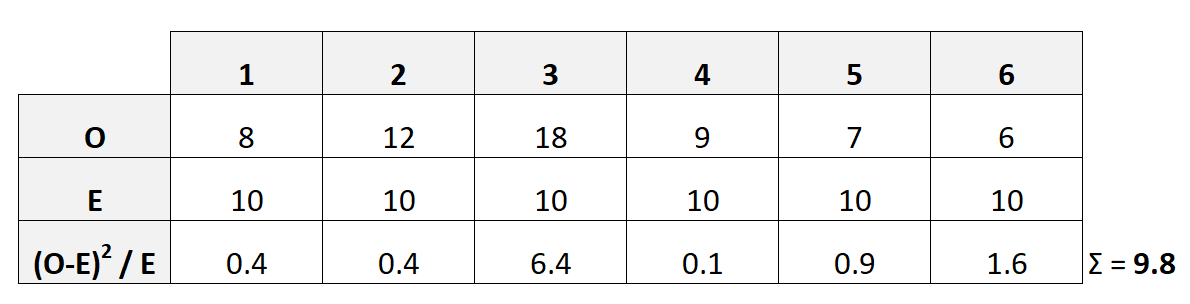
在这种情况下，X ²结果为9.8 。

第四步：找到临界值

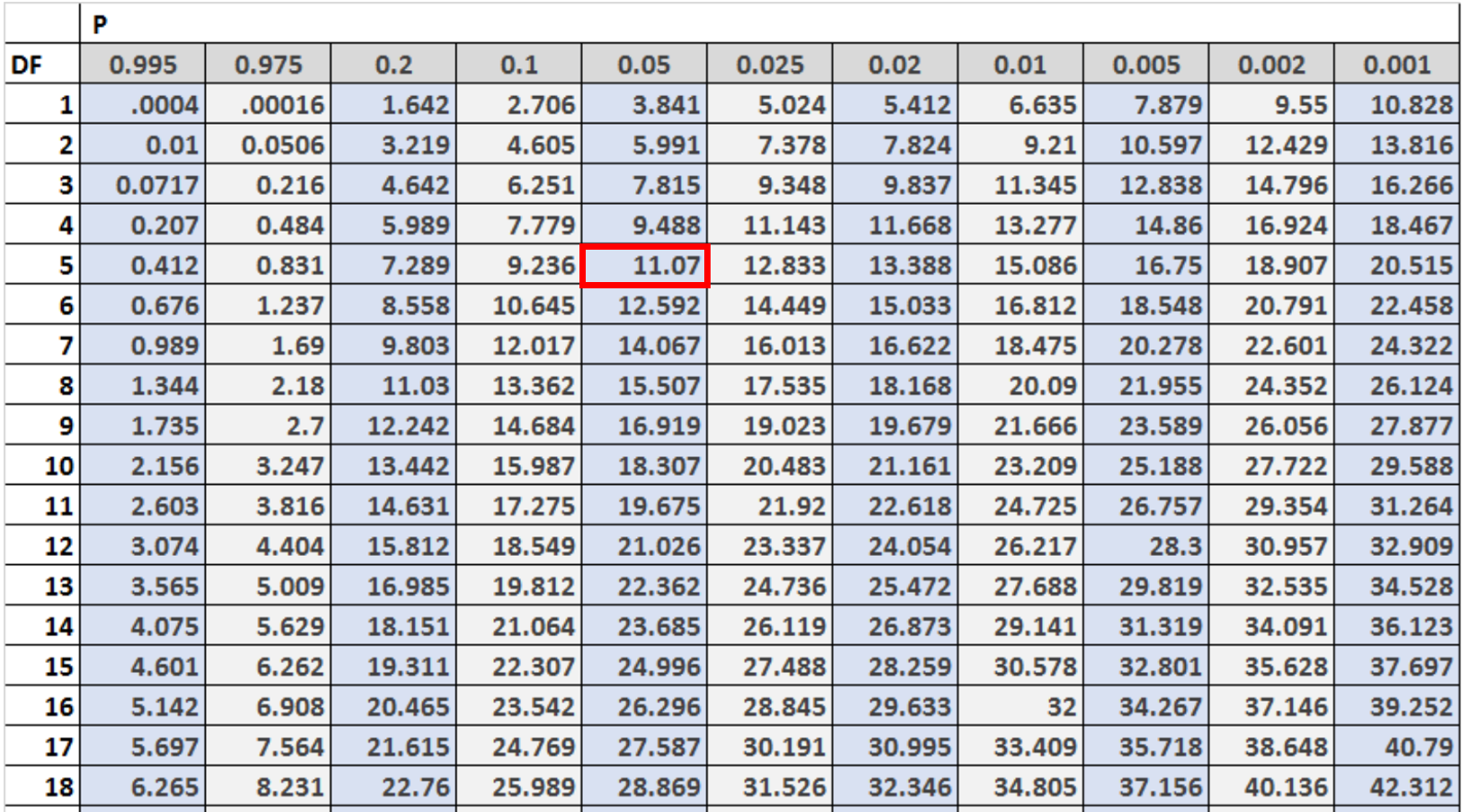
接下来，我们需要在卡方分布表中找到对应于 α = 0.05和 df = (#categories – 1) 的临界值。

在本例中，有 6 个类别，因此我们将使用 df = 6 – 1 = 5 。

我们可以看到临界值为11.07 。

步骤 5：拒绝或未能拒绝原假设

由于我们的检验统计量小于临界值，因此我们无法拒绝原假设。这意味着我们没有足够的证据表明骰子不公平。

其他资源

以下资源提供了有关卡方拟合优度检验的更多信息：

卡方拟合优度检验简介
如何在 R 中执行卡方拟合优度检验
卡方拟合优度检验计算器