如何查找给定区域的 z 分数（附示例）

可通过三种方法查找正态分布曲线下给定面积对应的 z 分数

1.使用 z 表。

2.使用 Z 分数百分位计算器。

3.在 TI-84 计算器上使用 invNorm() 函数。

以下示例演示如何使用每种方法来查找与正态分布曲线下给定面积相对应的 z 分数。

例1：求左边Z分数给定的区域

找到代表左侧分布区域 15.62% 的 z 分数。

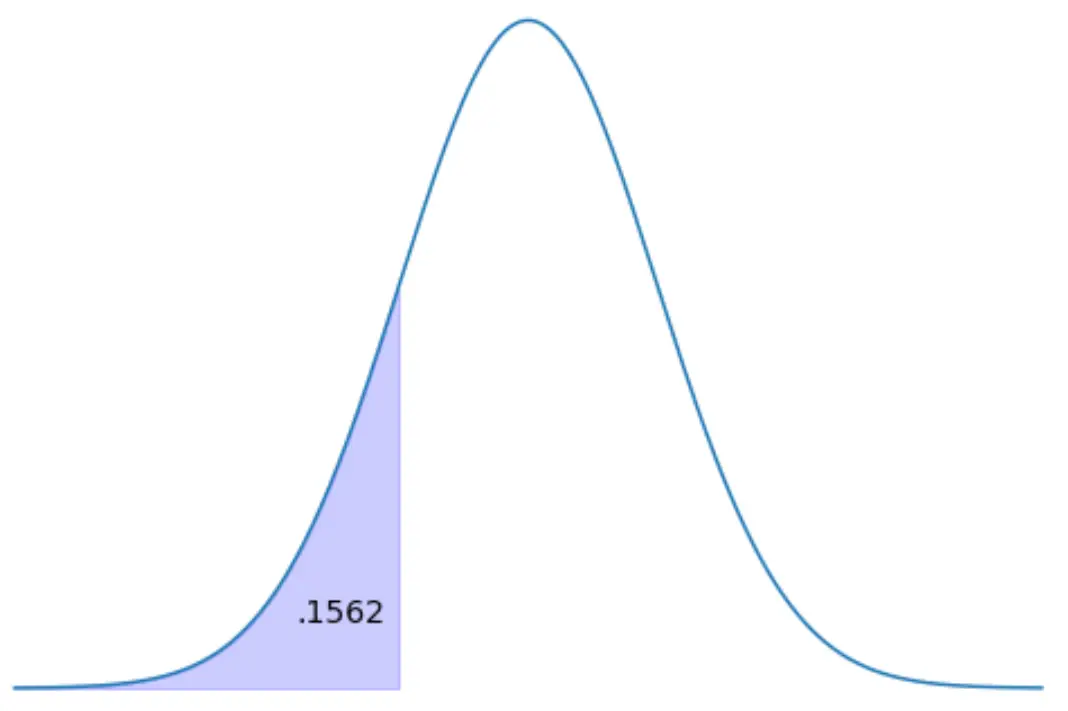
方法1：使用z表。

与 z 表中的值 0.1562 对应的 z 分数是-1.01 。

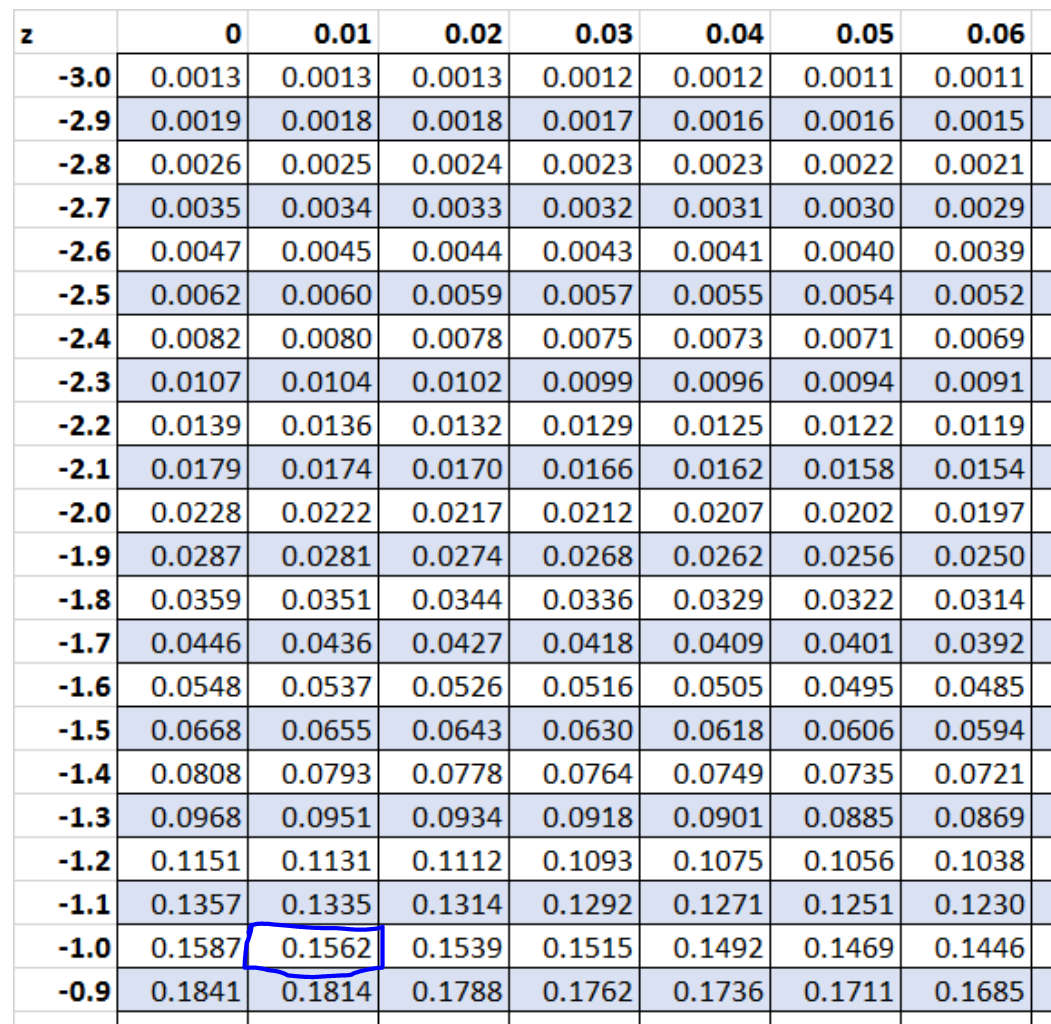
2. 使用 Z 分数百分位计算器。

根据 Z 分数百分位数计算器，百分位数 0.1562 对应的 z 分数是-1.01 。

3. 在 TI-84 计算器上使用 invNorm() 函数。

使用 TI-84 计算器上的invNorm() 函数，左侧 0.1562 区域对应的 z 分数为-1.01 。

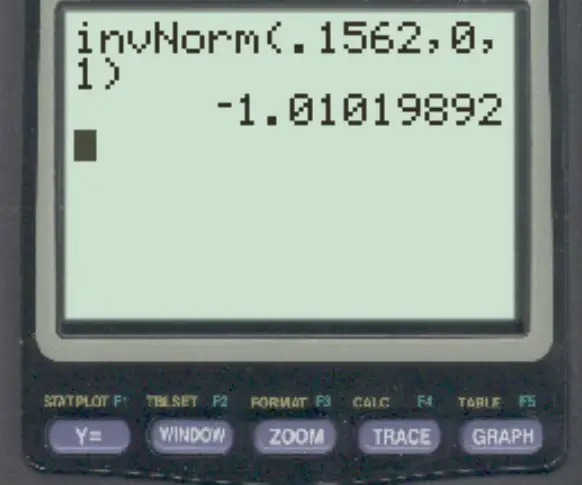
请注意，所有三种方法都会产生相同的结果。

例2：求右侧Z分数给定的区域

找到代表右侧分布区域 37.83% 的 z 分数。

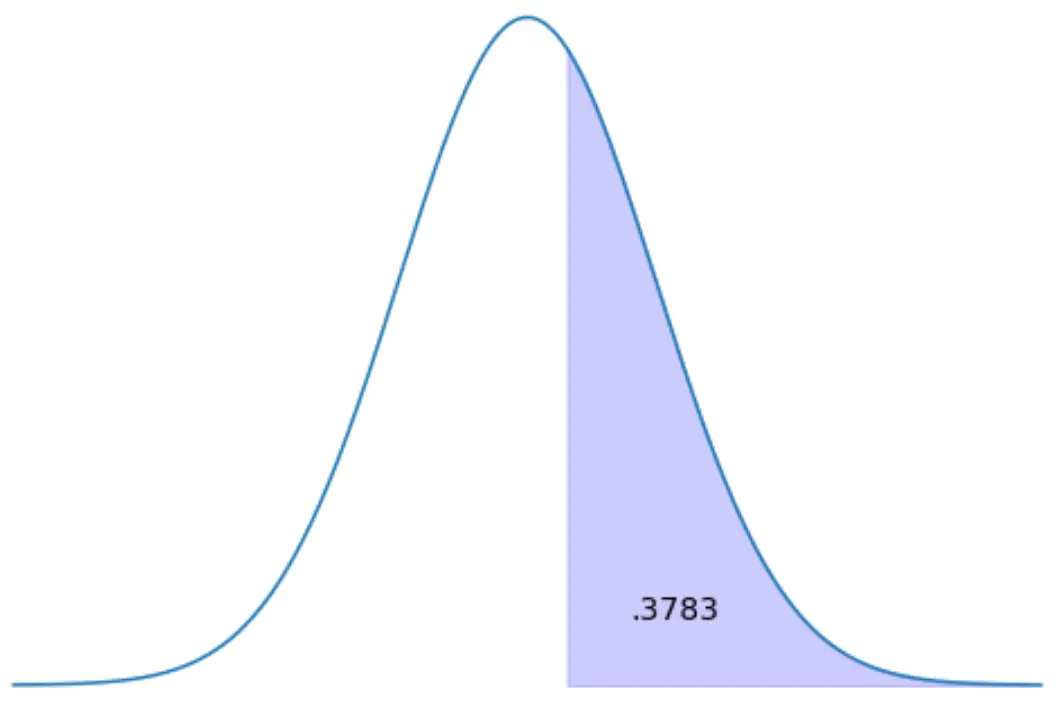
方法1：使用z表。

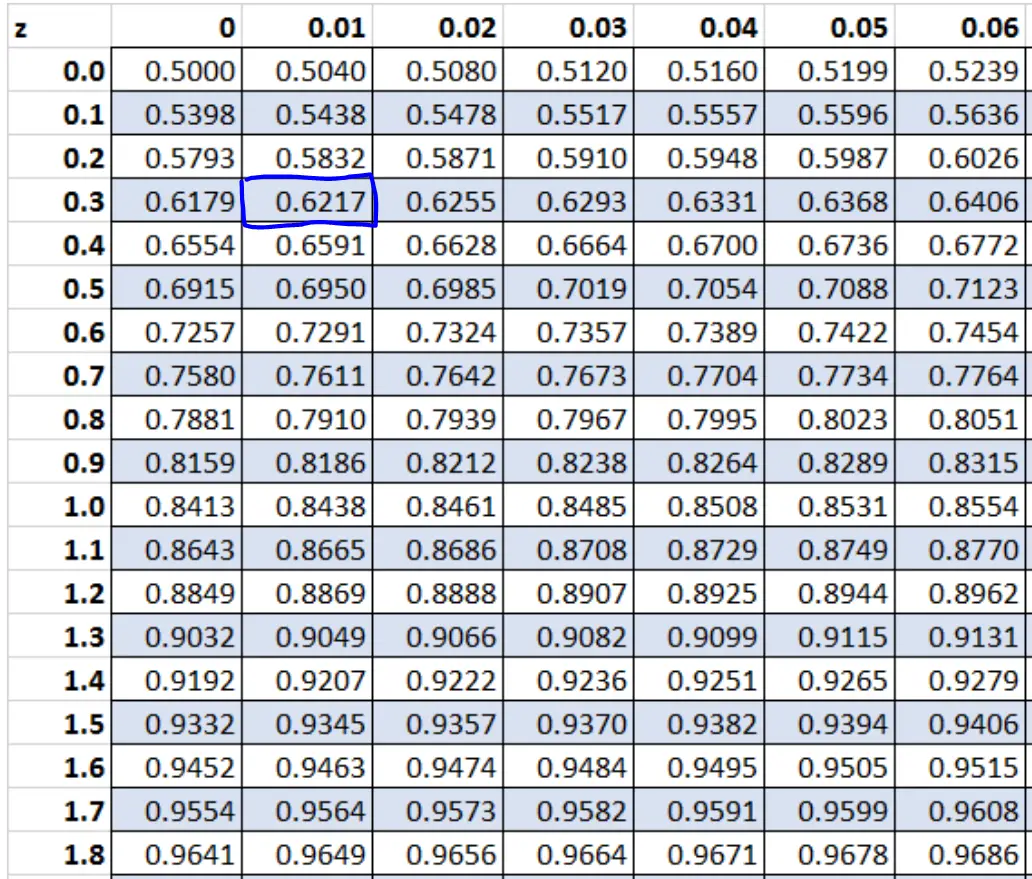
z 图表显示不同 z 分数左侧的区域。因此，如果我们知道右侧的面积为 0.3783，则左侧的面积为 1 – 0.3783 = 0.6217。

z 表中与值 0.6217 对应的 z 分数是0.31。

2. 使用 Z 分数百分位计算器。

根据 Z 分数百分位数计算器，百分位数 0.6217 对应的 z 分数为 。第3099章

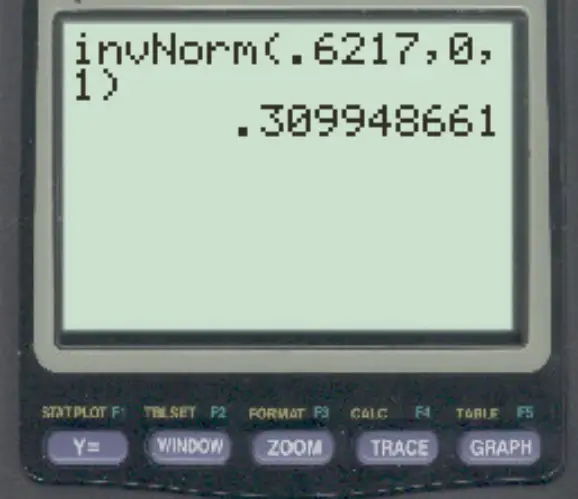
3. 在 TI-84 计算器上使用 invNorm() 函数。

在 TI-84 计算器上使用invNorm() 函数，左侧 0.6217 区域对应的 z 分数为0.3099 。

示例 3：查找两个值之间区域的 Z 分数

查找其间分布面积达到 95% 的 z 分数。

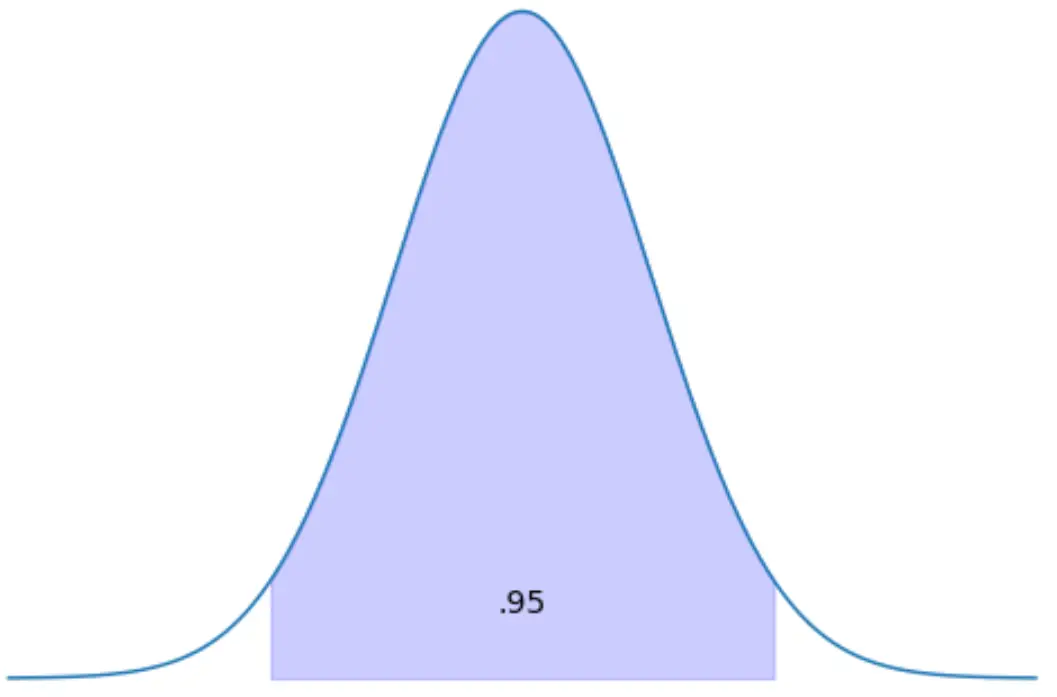
方法1：使用z表。

如果 95% 的分布位于两个 z 分数之间，则意味着 5% 的分布位于 z 分数之外。

因此，2.5% 的分布低于其中一个 z 分数，2.5% 的分布高于另一个 z 分数。

所以我们可以在z表中查找0.025。 z 表中对应于 0.025 的 z 分数是-1.96 。

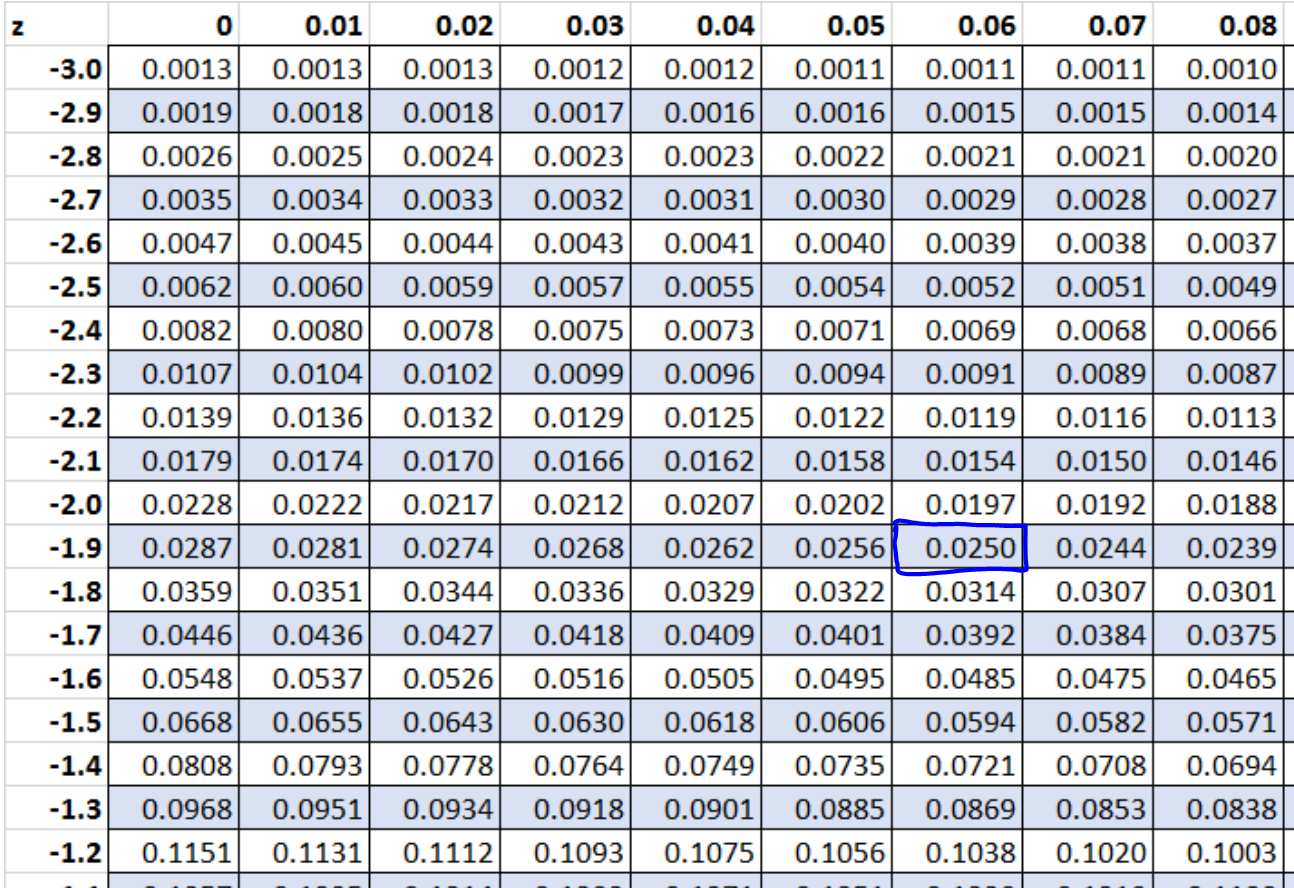
因此，包含它们之间 95% 分布的 z 分数为-1.96和1.96 。

2. 使用 Z 分数百分位计算器。

根据 Z 分数百分位数计算器，百分位数 0.025 对应的 z 分数为-1.96 。

因此，包含它们之间 95% 分布的 z 分数为-1.96和1.96 。

3. 在 TI-84 计算器上使用 invNorm() 函数。

在 TI-84 计算器上使用invNorm() 函数，左侧 0.025 区域对应的 z 分数为-1.96 。

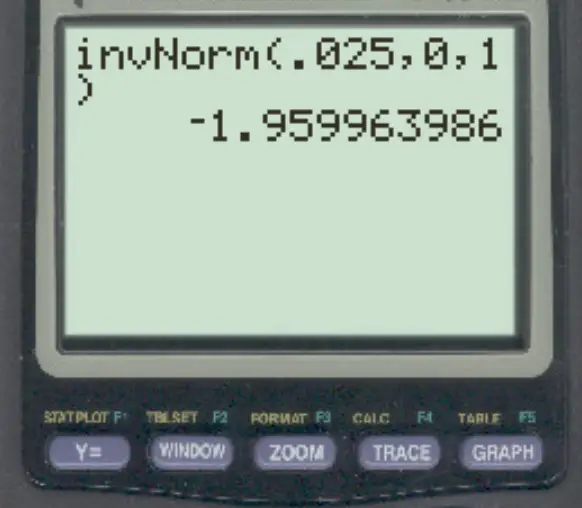
因此，包含它们之间 95% 分布的 z 分数为-1.96和1.96 。