抽样分配
本文解释了统计学中的抽样分布是什么以及它的用途。因此,您将了解抽样分布的含义、抽样分布的具体示例,以及最常见类型抽样分布的公式。
什么是抽样分布?
抽样分布或抽样分布是考虑总体中所有可能样本而得出的分布。换句话说,抽样分布是通过计算总体中所有可能样本的抽样参数得到的分布。
例如,如果我们从统计总体中提取所有可能的样本并计算每个样本的均值,则样本均值集合形成抽样分布。更准确地说,由于计算的参数是算术平均值,因此它是平均值的抽样分布。
在统计学中,抽样分布用于计算研究单个样本时接近总体参数值的概率。同样,抽样分布允许我们估计给定样本量的抽样误差。
抽样分布示例
现在我们知道了抽样分布的定义,让我们看一个简单的例子来充分理解这个概念。
- 在一个盒子里,我们放入三个球,每个球都有一个从 1 到 3 的数字,这样一个球的数字为 1,另一个球的数字为 2,最后一个球的数字为 3。对于大小为 n = 的样本2、如果选择有放回的样本,则计算均值的抽样分布的概率。
样本的选择是放回的,即拾取样本中第一个元素的球返回到盒子中,并可以在第二次提取时再次选择。因此,总体中所有可能的样本为:
1.1 1.2 1.3
2.1 2.2 2.3
3.1 3.2 3.3
因此,我们计算每个可能样本的算术平均值:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
因此,从总体中随机选取样本时,获得样本均值各值的概率如下:
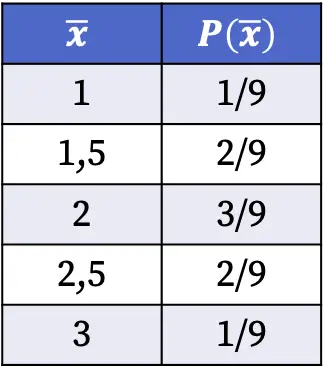
上表中所示的抽样分布的概率是通过将具有所述平均值的样本数量除以可能情况的总数来计算的。例如:在九种可能的情况下,样本平均值有两种为 1.5,因此 P(1.5)=2/9。
抽样分布的类型
抽样分布(或抽样分布)可以根据获得抽样参数的抽样参数进行分类。因此,最常见的分布类型如下:
- 均值抽样分布:这是通过计算每个样本的算术平均值而得到的抽样分布。
- 比例抽样分布:是通过计算所有样本的比例得到的抽样分布。
- 方差抽样分布:这是形成样本中所有方差集合的抽样分布。
- 均值差异抽样分布:是通过计算两个不同总体的所有可能样本的均值之间的差异而得出的抽样分布。
- 比例抽样分布差异:是通过从两个总体中减去所有可能的抽样比例而获得的抽样分布。
下面更详细地解释了每种类型的抽样分布。
均值的抽样分布
给定一个服从正态概率分布且均值为
![]()
和标准差
![]()
并提取尺寸样本
![]()
,均值的抽样分布也将由具有以下特征的正态分布定义:
![Rendered by QuickLaTeX.com \begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-44571aa7337b095ab9c9fa1f746e93a5_l3.png)
金子
![]()
是平均值的抽样分布的平均值,
![]()
是它的标准差。此外,
![]()
是抽样分布的标准误。
注:如果总体不服从正态分布但样本量较大(n>30),均值的抽样分布也可以通过中心定理极限逼近上面的正态分布。
因此,由于均值的抽样分布遵循正态分布,因此计算与样本均值相关的任何概率的公式为:

金子:
-

是样本均值。
-

这是人口平均值。
-

是总体标准差。
-

是样本大小。
-

是由标准正态分布 N(0,1) 定义的变量。
比例抽样分配
事实上,当我们研究一部分样本时,我们是在分析成功案例。因此,研究中的随机变量服从二项式概率分布。
根据中心极限定理,对于大尺寸(n>30),我们可以使二项式分布更接近正态分布。因此,比例的抽样分布近似于具有以下参数的正态分布:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-f3408076893f390bb65baecfe38e6eff_l3.png)
金子
![]()
是成功的概率,
![]()
是失败的概率
![]()
。
注意:二项式分布只能近似于正态分布,如果

![]()
和
![]()
。
因此,由于比例的抽样分布可以近似为正态分布,因此计算与样本比例相关的任何概率的公式为:

金子:
-

是样本比例。
-

是人口的比例。
-

是总体失败的概率,

。
-

是样本大小。
-

是由标准正态分布 N(0,1) 定义的变量。
方差抽样分布
方差的抽样分布由卡方概率分布定义。因此,抽样方差分布的统计公式为:
![]()
金子:
-

是方差抽样分布的统计量,遵循卡方分布。
-

是样本大小。
-

是样本方差。
-

是总体方差。
均值差的抽样分布
如果样本量足够大(n 1 ≥30且n 2 ≥30),则均差的抽样分布服从正态分布。更准确地说,所述分布的参数计算如下:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-90c67b74b4e9326b7869d641a59725d9_l3.png)
注意:如果两个总体都是正态分布,则无论样本大小如何,均值差的抽样分布都遵循正态分布。
因此,由于均值差的抽样分布是由正态分布定义的,因此均值差的抽样分布统计量的计算公式为:

金子:
-

是样本 i 的平均值。
-

是总体 i 的平均值。
-

是总体 i 的标准差。
-

是样本大小 i。
-

是由标准正态分布 N(0,1) 定义的变量。
请注意,来自不同人群的样本可能具有不同的样本量。
比例差异抽样分布
为比例抽样分布差异选择的样本由二项式分布定义,因为出于实际目的,比例是成功案例与观察总数的比率。
然而,由于中心极限定理,二项式分布可以近似为正态概率分布。因此,比例差异的抽样分布可以近似为具有以下特征的正态分布:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-a1ce359b5dd6d80f8d27b0b9a1034bed_l3.png)
注:比例差异的抽样分布只能近似于正态分布,如果
![]()
,
![]()
,
![]()
,
![]()
,
![]()
和
![]()
。
因此,由于比例差的抽样分布可以近似为正态分布,因此比例差的抽样分布统计量的计算公式为:

金子:
-

是样本比例 i。
-

是人口 i 的比例。
-

是群体 i 失败的概率,

。
-

是样本大小 i。
-

是由标准正态分布 N(0,1) 定义的变量。