抽样方法的类型（附示例）

研究人员经常想回答有关人群的问题，例如：

• 某种植物种类的平均高度是多少？
• 某种鸟类的平均重量是多少？
• 某个城市有多少比例的公民支持某项法律？

回答这些问题的一种方法是收集感兴趣人群中每个人的数据。

然而，这通常成本过高且耗时，因此研究人员改为对总体进行抽样，并使用样本数据得出有关总体总体的结论。

研究人员可以使用许多不同的方法将个体纳入样本。这些方法称为抽样方法。

在本文中，我们分享了统计学中最常用的抽样方法，包括不同方法的优点和缺点。

概率抽样方法

第一类抽样方法称为概率抽样方法，因为总体中的每个成员都有相同的概率被选择进入样本。

简单随机样本

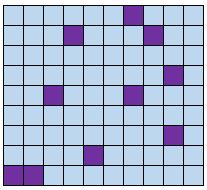
定义：总体中的每个成员都有平等的机会被选为样本的一部分。使用随机数生成器或随机选择方法随机选择成员。

例子：我们把班级每个学生的名字放进帽子里，随机抽取名字，得到学生样本。

优点：简单的随机样本通常可以代表感兴趣的总体，因为每个成员都有平等的机会被包含在样本中。

分层随机样本

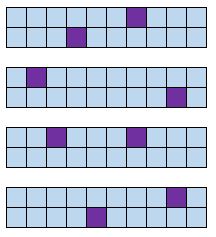
定义：将人口分为几组。从每个组中随机选择一些成员作为样本的一部分。

示例：将学校的所有学生按照年级分为：一年级、二年级、三年级和四年级。让每个年级 50 名学生完成一项有关学校膳食的调查。

优点：分层随机样本确保每个人群的成员都包含在调查中。

聚类随机样本

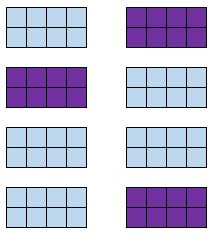
定义：将群体划分为集群。随机选择一些簇并将这些簇的所有成员包含在样本中。

示例：一家提供观鲸之旅的公司想要对其客户进行调查。在他们每天提供的十个旅游团中，他们随机选择四个旅游团，并向每位顾客询问他们的体验。

优点：聚类随机样本收集某些组的所有成员，这在每个组反映整体总体时非常有用。

系统随机抽样

定义：将总体中的每个成员按一定的顺序排列。选择一个随机起点并选择每个^{第 n 个}成员作为样本的一部分。

示例：教师按姓氏字母顺序对学生进行排序，随机选择一个起点，然后选择每五个学生作为样本。

优点：系统随机样本通常能够代表感兴趣的总体，因为每个成员都有平等的机会被纳入样本。

非概率抽样方法

另一类抽样方法称为非概率抽样方法，因为并非总体中的所有成员都具有相同的被选择进入样本的概率。

有时会使用这种类型的抽样方法，因为它比概率抽样方法更便宜且更实用。当研究人员只是想初步了解某个群体时，通常会在探索性分析中使用它。

然而，这些抽样方法产生的样本不能用于得出有关它们所抽取的总体的结论，因为它们通常不是代表性样本。

方便样品

定义：选择人群中容易获得的成员纳入样本。

示例：一名研究人员白天站在图书馆前采访路人。

缺点：地点和时间会影响结果。样本很可能会受到低估偏差的影响，因为有些人（例如白天工作的人）不会像样本中所代表的那样。

自愿回应样本

定义：研究人员要求志愿者参与研究，群体成员自愿决定是否纳入样本。

示例：一位电台主持人要求听众上网并在他的网站上完成一项调查。

缺点：自愿回应的人可能比其他人有更强烈的意见（正面或负面），使他们成为不具有代表性的样本。通过使用这种抽样方法，样本可能会遭受无答复偏差——某些人群根本不太可能提供答复。

雪球样本

定义：研究人员招募初始受试者参与研究，然后要求这些初始受试者招募更多受试者参与研究。使用这种方法，随着每个额外的受试者招募更多受试者，样本量会越来越大。

示例：研究人员正在对患有罕见疾病的人进行研究，但很难找到真正患有这种疾病的人。然而，如果他们能够找到最初的几个人参与研究，那么他们可以要求他们通过私人支持小组或其他方式招募他们可能认识的其他人。

缺点：容易出现抽样偏差。由于最初的受试者招募了更多受试者，因此许多受试者可能具有相似的特征或特征，而这些特征或特征可能无法代表更广泛的研究人群。因此，样本结果不能外推到总体。

在此处了解有关滚雪球采样的更多信息。

纯样品

定义：研究人员根据他们认为对他们的研究目标最有用的人来招募人员。

示例：研究人员想了解城镇居民对在城镇广场安装新攀岩馆的可能性的看法。所以他们特意寻找经常光顾城里其他攀岩馆的人。

缺点：样本中的个体不太可能代表总体。因此，样本结果不能外推到总体。