指数分布

本文解释了统计学中的指数分布是什么以及它的用途。同样，您会发现指数分布的属性及其公式、图表和已解决的练习。此外，您将能够使用在线指数分布计算器计算任何概率。

什么是指数分布？

指数分布是一种连续概率分布，用于对随机现象发生的等待时间进行建模。

更准确地说，指数分布使我们能够描述遵循泊松分布的两个事件之间的等待时间。因此，指数分布与泊松分布密切相关。

指数分布有一个特征参数，用希腊字母 λ 表示，表示所研究的事件在给定时间段内预计发生的次数。

同样，指数分布也用于对故障发生之前的时间进行建模。因此，指数分布在可靠性和生存理论中有多种应用。

指数分布的示例

现在我们已经知道了指数分布的定义，让我们看一下这种分布的几个例子，以更好地理解这个概念。

指数分布的示例：

1. 呼叫中心两次呼叫之间经过的时间。
2. 一个人必须等待免费出租车经过特定街道的时间。
3. 新顾客进入商店之前的等待时间。
4. 两个不同用户进入网页之间所经过的时间。
5. 机场从一架飞机起飞到另一架飞机起飞之间所经过的时间。

指数分布公式

定义指数分布概率计算的密度函数公式等于 λ 乘以数字 e 的负 λ 次方乘以 x。

换句话说，指数分布概率的计算公式如下：

👉您可以使用下面的计算器来计算变量服从指数分布的概率。

另一方面，计算指数分布累积概率的公式如下：

指数分布图

在本节中，您可以看到指数分布的密度函数和分布函数的图形表示。

下面您可以看到指数分布的密度函数图如何根据参数 λ 的值而变化。

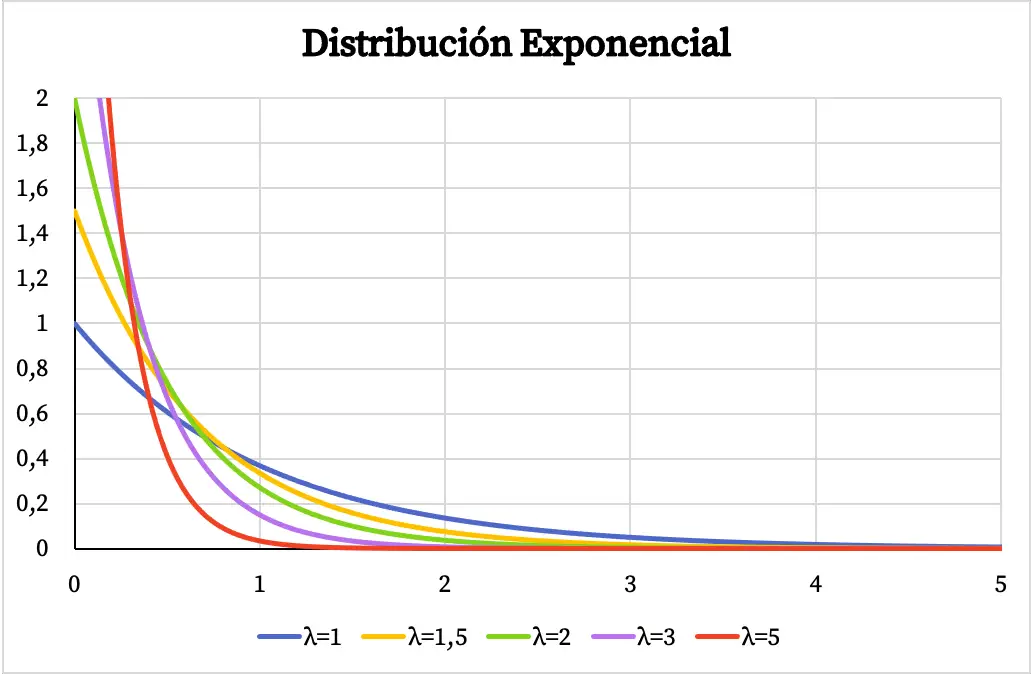
同样，指数分布的累积概率函数也取决于参数 λ 的值，如下图所示：

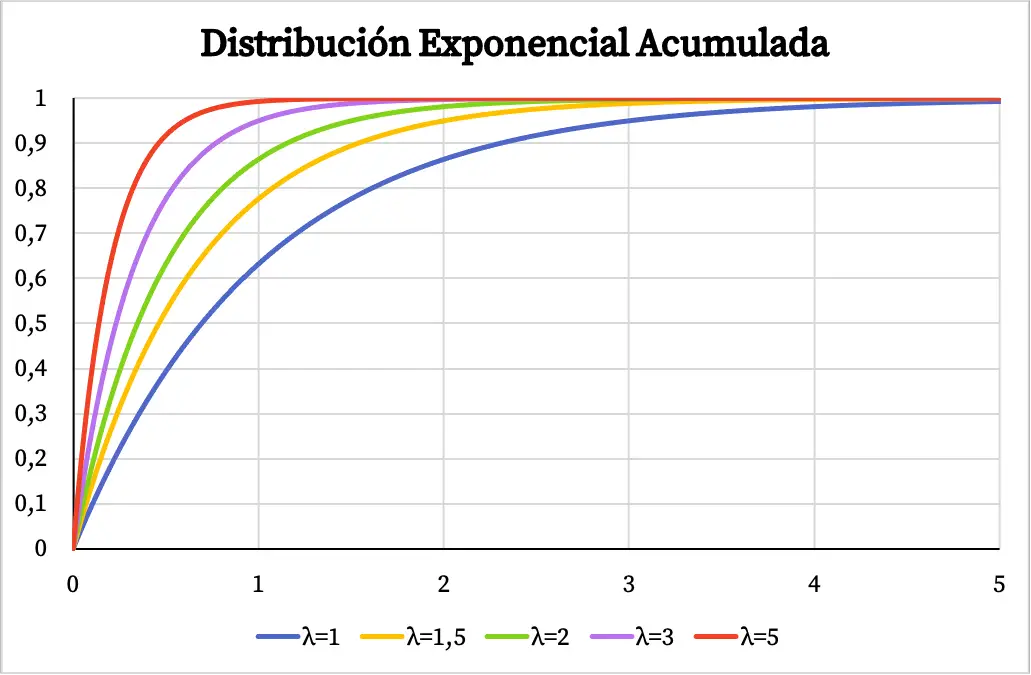
解答了指数分布的练习

• 平均而言，λ=1 个用户/分钟访问特定网页。两个用户进入之间的时间间隔为 3 分钟的概率是多少？那么等于或小于2分钟的概率是多少？

定义该问题的随机变量的分布是指数分布，因为我们研究从事件发生（用户进入网页）到同一事件再次发生所经过的时间。

因此，要计算两个不同用户进入之间所经过的时间为三分钟的概率，我们需要应用密度函数公式（见上文）：

另一方面，为了确定累积概率，我们必须使用指数分布的分布函数公式：

指数分布的特征

指数分布具有以下特点：

• 指数分布有一个特征参数 λ，它表示所研究的现象在给定时间段内预计发生的次数。

• 指数分布不能取负值，因此指数分布的域由所有大于或等于零的实数组成。

• 指数分布的平均值等于一除以特征参数 λ。

• 指数分布的方差是其均值的平方，因此指数分布的方差等于系数 λ 平方的 1。

• 无论 λ 的值是多少，指数分布的不对称系数始终等于 2。

• 同样，任何指数分布的峰度系数始终等于 9。

• 指数分布的密度函数的公式为：

• 而指数分布的累积概率函数的公式如下：

• 指数分布是少数具有内存不足特性的概率分布之一。该属性意味着先前事件的发生不会影响该事件将来发生的概率。例如，在指数分布中，新用户在不到一分钟内访问网页的概率并不取决于用户是刚刚进入还是此后没有用户进入。十多分钟。

指数分布计算器

将参数λ的值和x的值输入到下面的计算器中以计算概率。您需要选择要计算的概率，并使用点作为小数分隔符输入数字，例如 0.50。