如何在 python 中使用指数分布

指数分布是一种概率分布，用于对我们必须等待特定事件发生的时间进行建模。

如果随机变量X服从指数分布，则X的累积分布函数可以写为：

F (x; λ) = 1 – e ^-λx

金子：

• λ：速率参数（计算公式为 λ = 1/μ）
• e：约等于 2.718 的常数

本教程介绍如何在 Python 中使用指数分布。

如何生成指数分布

您可以使用 Python 中 SciPy 库中的expon.rvs(scale, size)函数从具有特定速率参数和样本大小的指数分布生成随机值：

 from scipy. stats import expo

#generate random values from exponential distribution with rate=40 and sample size=10
expon. rvs (scale= 40 , size= 10 )

array([116.5368323 , 67.23514699, 12.00399043, 40.74580584,
        34.60922432, 2.68266663, 22.70459831, 97.66661811,
         6.64272914, 46.15547298])

注意：您可以在此处找到完整的 SciPy 库文档。

如何使用指数分布计算概率

假设某个间歇泉喷发的平均分钟数为 40 分钟。我们等待不到 50 分钟就会爆发的可能性有多大？

为了解决这个问题，我们首先需要计算速率参数：

• λ = 1/μ
• λ = 1/40
• λ = 0.025

我们可以将 λ = 0.025 和 x = 50 代入 CDF 公式：

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 50) = 1 – e ^-0.025(50)
• P(X≤50)=0.7135

我们需要等待不到 50 分钟才能看到下一次喷发的概率是0.7135 。

我们可以在Python中使用SciPy的expon.cdf()函数来解决这个问题：

 from scipy. stats import expo

#calculate probability that x is less than 50 when mean rate is 40
expon. cdf (x=50, scale=40)

0.7134952031398099

我们需要等待不到 50 分钟才能看到下一次喷发的概率是0.7135 。

这对应于我们手动计算的值。

如何绘制指数分布

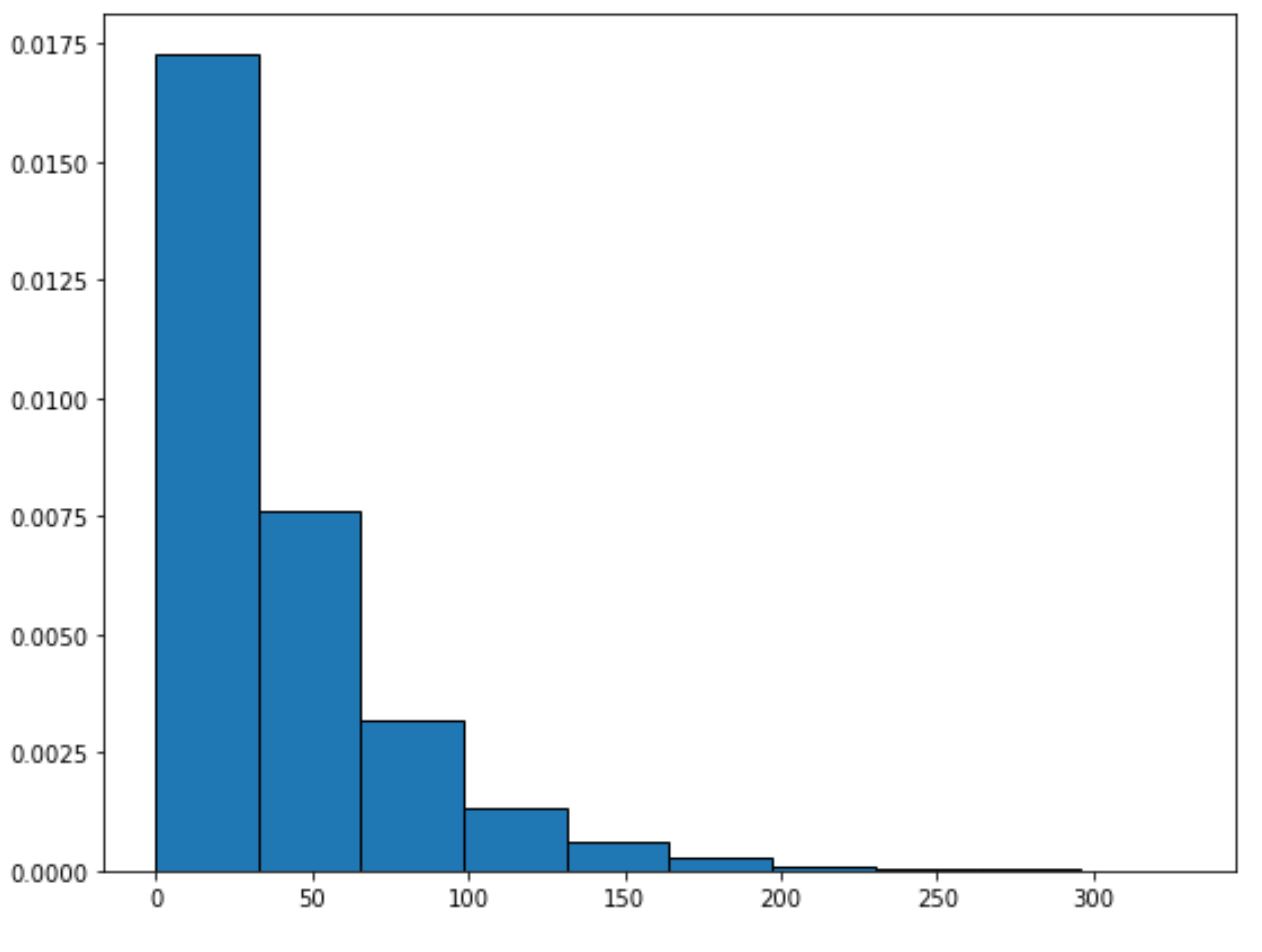
您可以使用以下语法来绘制具有给定速率参数的指数分布：

 from scipy. stats import expo
import matplotlib. pyplot as plt

#generate exponential distribution with sample size 10000
x = expon. rvs (scale= 40 ,size= 10000 )

#create plot of exponential distribution
plt. hist (x, density= True , edgecolor=' black ')

其他资源

以下教程解释了如何在 Python 中使用其他常见发行版：

如何在Python中使用泊松分布
如何在Python中使用t分布
如何在 Python 中使用均匀分布