如何在excel中使用指数分布

指数分布是一种概率分布，用于对我们必须等待特定事件发生的时间进行建模。

该分布可用于回答以下问题：

• 零售商应该等待顾客进入商店多久？
• 电池在耗尽之前还能继续工作多长时间？
• 计算机在损坏之前还能继续工作多长时间？

在每种情况下，我们想要计算需要等待多长时间才能发生特定事件。因此，每个场景都可以使用指数分布进行建模。

如果随机变量X服从指数分布，则X的累积密度函数可以写为：

F (x; λ) = 1 – e ^-λx

金子：

• λ：速率参数（计算公式为 λ = 1/μ）
• e：约等于 2.718 的常数

为了计算Excel中指数分布的累积密度函数相关的概率，我们可以使用以下公式：

 =EXPON.DIST(x, lambda, cumulative)

金子：

• x ：指数分布随机变量的值
• lambda ：速率参数
• cumulative ：是否使用累积密度函数（TRUE或FALSE）

以下示例展示了如何在实践中使用该公式。

示例 1：距下一位顾客到达的时间

平均每两分钟就有一位新顾客进入商店。客户到达后，确定新客户在一分钟内到达的概率。

解决方案：顾客之间的平均时间是两分钟。因此，该比率可以计算如下：

• λ = 1/μ
• λ = 1/2
• λ = 0.5

因此，我们可以在 Excel 中使用以下公式来计算新客户在一分钟内到达的概率：

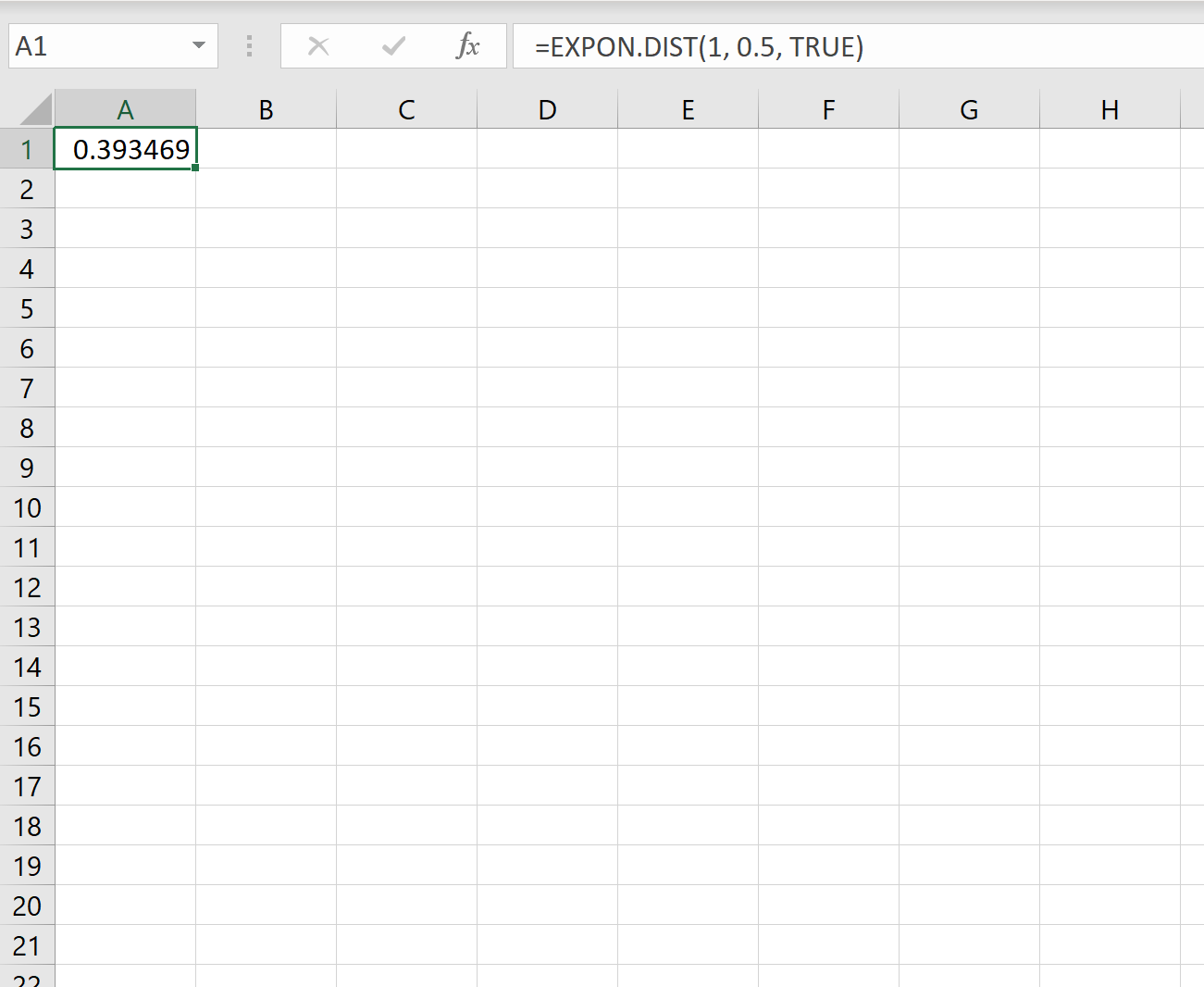
我们需要等待不到一分钟才能下一位顾客到达的概率是0.393469 。

示例 2：距下一次地震的时间

假设某个地区平均每 400 天就会发生一次地震。地震发生后，确定距离下一次地震发生 500 天以上的概率。

解：地震的平均间隔时间是400天。因此，该比率可以计算如下：

• λ = 1/μ
• λ = 1/400
• λ = 0.0025

因此，我们可以在Excel中使用以下公式来计算下一次地震发生时间小于500天的概率：

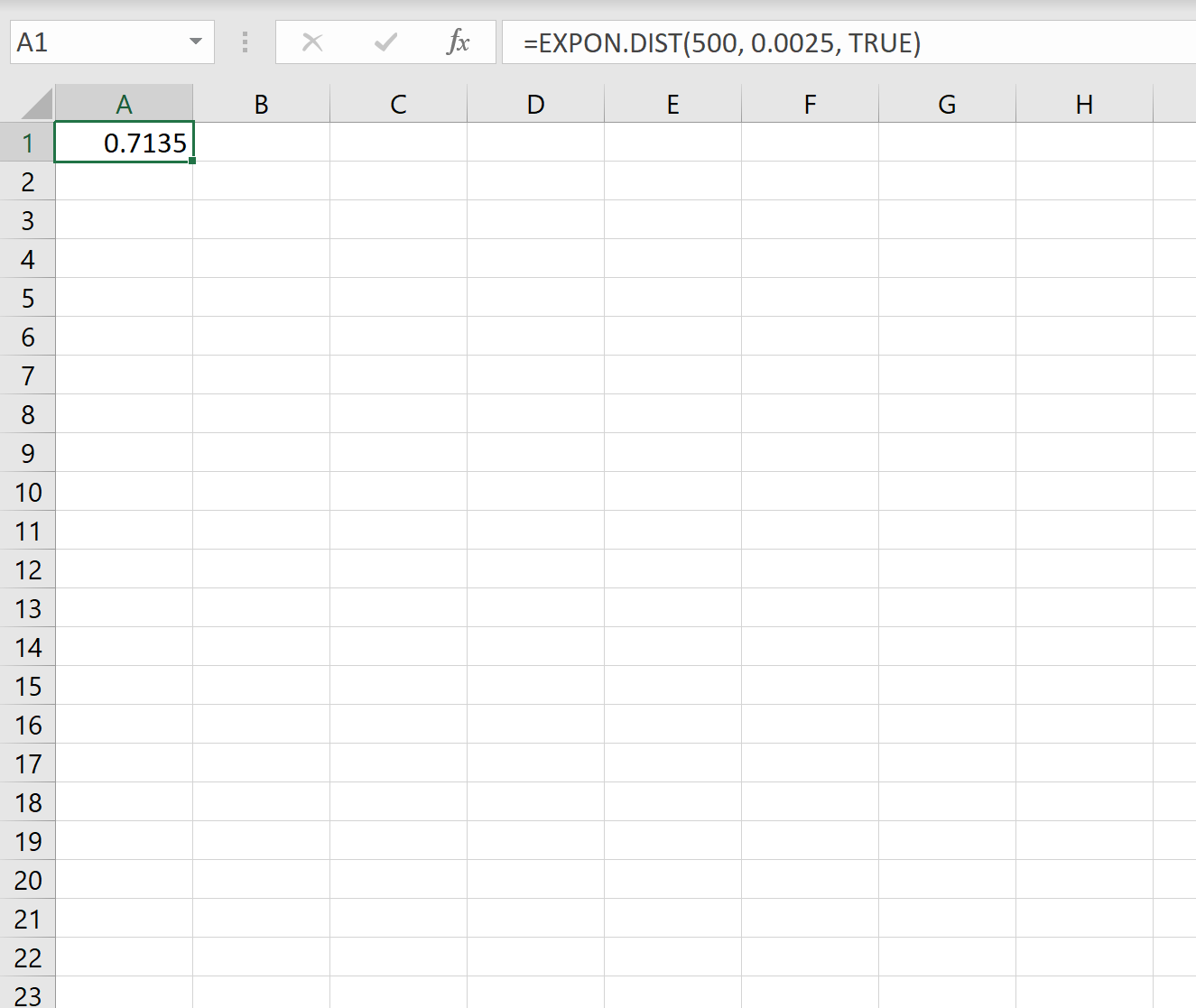
距离下一次地震不到 500 天的概率为 0.7135。

因此，我们需要等待 500 天以上才能发生下一次地震的概率是 1 – 0.7135 = 0.2865 。

示例 3：距下一次电话的时间

假设呼叫中心平均每 10 分钟就会接到一个新电话。客户致电后，确定新客户在 10 到 15 分钟内致电的可能性。

解决方案：呼叫之间的平均时间为 10 分钟。因此，该比率可以计算如下：

• λ = 1/μ
• λ = 1/10
• λ = 0.1

因此，我们可以在Excel中使用以下公式来计算下一个客户在10到15分钟内打电话的概率：

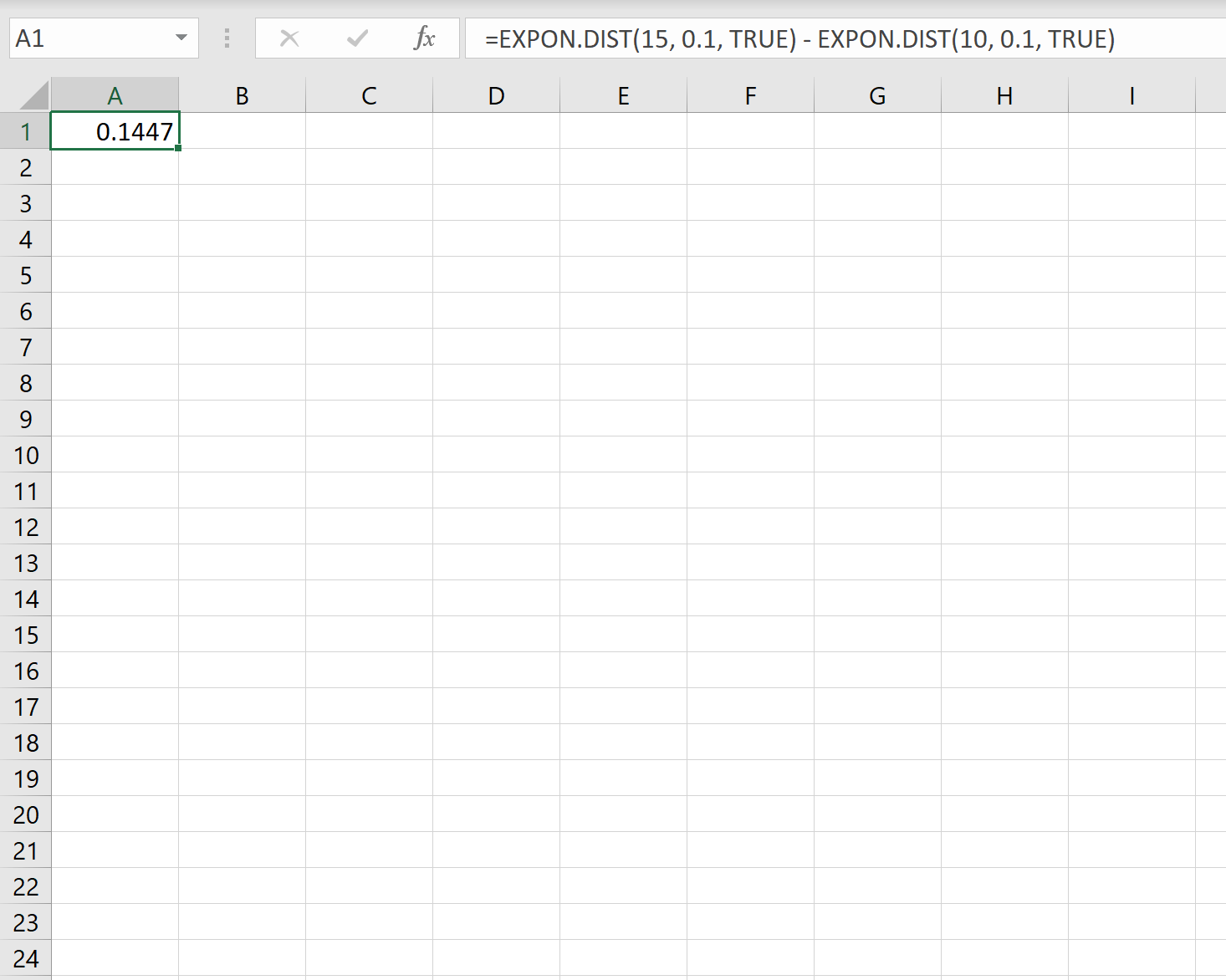
新客户在 10-15 分钟内致电的可能性。是0.1447 。

其他资源

指数分布简介
指数分布的无记忆特性
如何在 R 中绘制指数分布