推理和预测:有什么区别?
在统计中,我们通常出于以下两个原因之一使用数据:
(1) 推论:我们想要了解现有数据集中预测变量和响应变量之间关系的本质。
(2) 预测:我们希望使用现有的数据集构建一个模型来预测新观察的响应变量的值。
例如,假设我们有以下包含房屋信息的数据集:
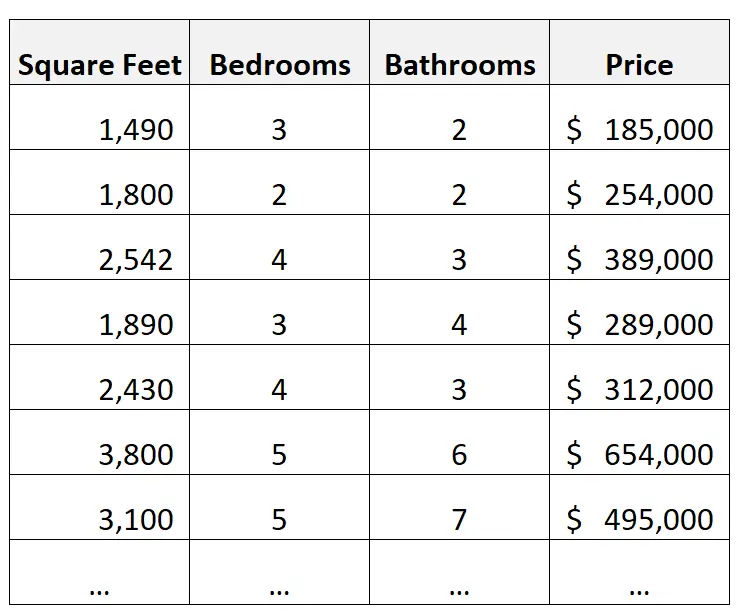
一个推理的例子:
假设我们使用平方英尺、卧室数量和浴室数量作为预测变量,使用价格作为响应变量来构建多元线性回归模型。
然后,我们可以使用回归系数来了解与每个预测变量的一个单位变化相关的平均价格变化。
例如,我们可以了解每增加一间卧室、每增加一间浴室以及每增加一平方英尺,价格会发生多少变化(平均)。
预测示例:
我们可以构建相同的多元线性回归模型,并使用它根据新房的平方英尺、卧室数量和浴室数量来预测新房的价值。
例如,我们可以使用该模型来预测 3 间卧室、3 间浴室、2,000 平方英尺的新房的价格。
然后,我们可以将我们的预测与实际挂牌价格进行比较,并评估房屋是否被低估或高估。
下面的例子说明了不同场景下推理和预测的区别:
示例1:体育运动中的推理和预测
假设我们有以下数据集,其中包含职业篮球队的信息:
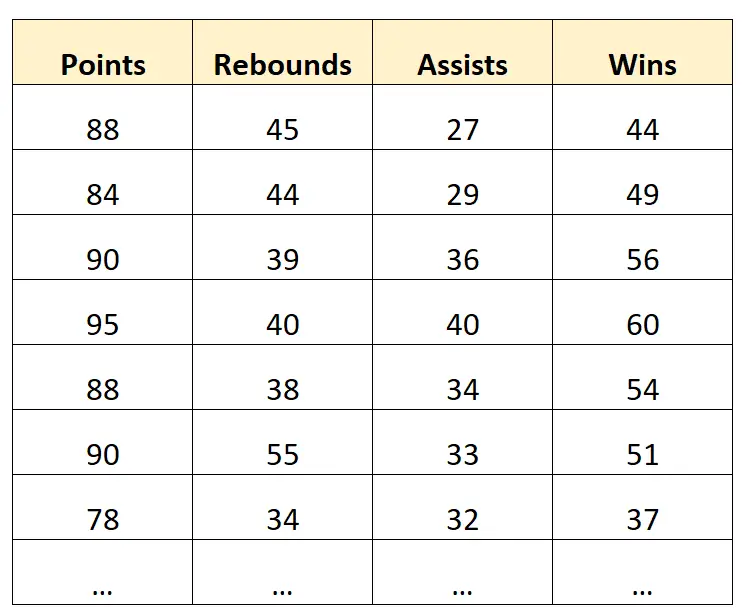
一个推理的例子:
假设我们使用得分、篮板和助攻作为预测变量,并使用胜利作为响应变量来构建多元线性回归模型。
然后,我们可以使用该模型来了解每次额外得分、篮板和助攻时获胜次数的变化(平均)有多少。
预测示例:
我们可以构建相同的多元线性回归模型,并使用它根据球队的得分、篮板和助攻数来预测球队将获得多少场胜利。
例如,我们可以使用该模型来预测一支得到 90 分、40 个篮板和 30 次助攻的球队将获得多少场胜利。
示例2:商业中的推理和预测
假设我们有以下数据集,其中包含各公司年收入(以百万计)的信息:
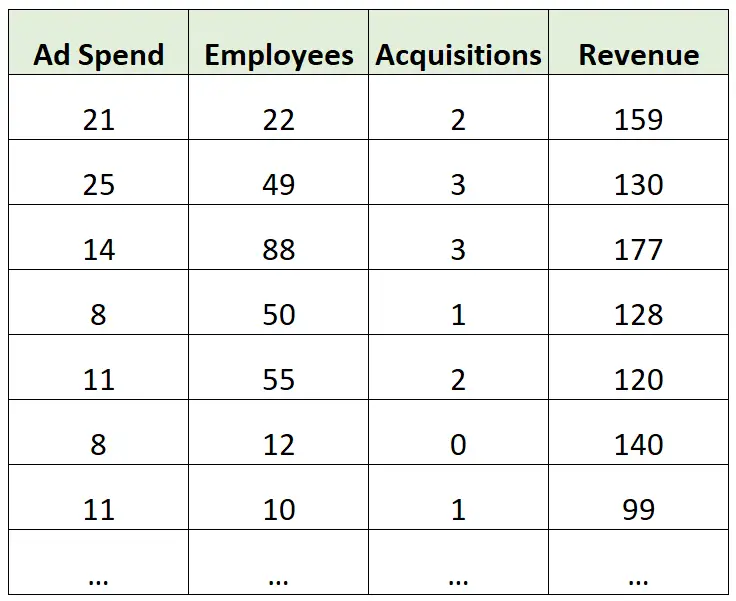
一个推理的例子:
假设我们使用广告支出、员工数量和总收购量作为预测变量,将年收入作为响应变量,构建一个多元线性回归模型。
然后,我们可以使用该模型来了解随着每增加一美元的广告支出、每增加一名员工以及每增加一次收购,年总收入会发生多少变化(平均)。
预测示例:
我们可以构建相同的多元线性回归模型,并使用它根据公司的营销总支出、员工数量和收购总额来预测公司的年收入。
例如,我们可以使用该模型来预测一家在广告上花费 2500 万美元、拥有 40 名员工并进行了 2 次收购的公司的年收入。
其他资源
以下教程提供了有关统计中需要理解的重要术语的附加信息:
描述性统计或推论性统计:有什么区别?
测量级别:名义、序数、间隔和比率
定性变量和定量变量:有什么区别?