放射状图（或蜘蛛图）

本文解释什么是径向图（也称为蜘蛛图）。因此，您将了解径向图的用途、它是如何制作的、构建径向图的具体示例，最后，这种统计图的优点和缺点是什么。

什么是径向图？

径向图，也称为蜘蛛图，是一种表示各种变量的统计图表。即在统计学中，径向图用于比较不同变量的值。

此外，径向图的主要优点是非常直观，可以轻松快速地比较变量。

径向图也称为网络图、极坐标图或星形图。

如何制作放射状图表

给出了径向图（或蜘蛛图）的定义，让我们看看这种类型的图是如何制作的。

1. 创建一个正多边形，其边数与要研究的统计变量一样多。
2. 创建更多与上一步相同类型但大小不同的多边形，以便每个多边形代表不同的值。
3. 将正多边形垂直和水平居中。
4. 正多边形的每个半径对应于不同变量的轴。
5. 绘制一个代表每个变量值的不规则多边形，使得不规则多边形的每个顶点在每个变量的轴上与该变量所取的值重合。
6. 为了更好地可视化径向图，您可以在不规则多边形内部进行绘制。

另一方面，目前有很多计算机软件程序可以让您快速构建径向图，例如Excel。

径向图示例

• 以放射状图（或蜘蛛图）表示一个人本学期在学校获得的成绩：

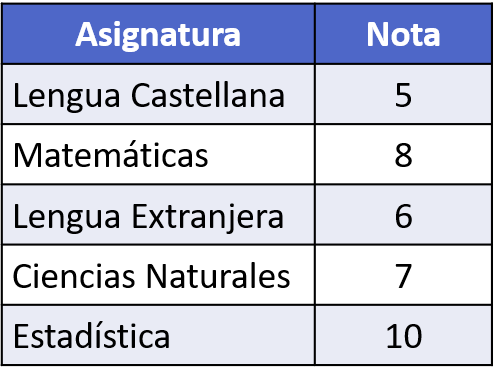
执行上述步骤后，给定数据集的蜘蛛图中的图形表示如下：

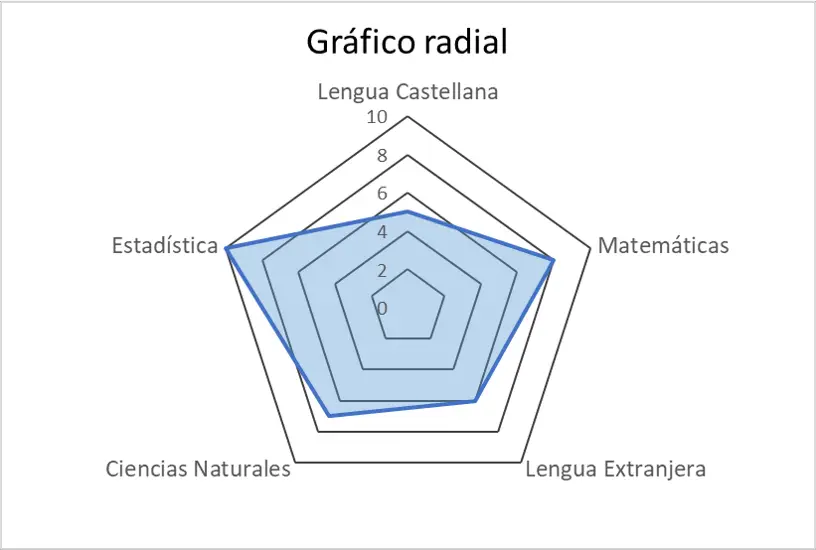
一旦我们构建了径向图，我们将对其进行解释。从图中可以看出，该学生在数字学科上取得了比文学学科更好的成绩。从径向图可以清楚地看出，统计和数学的分数高于语言的分数。

雷达图的优缺点

由于放射状图（或星状图）的特点，它们具有以下优点和缺点：

优势：

• 这是一种非常直观且有吸引力的图表类型。
• 它允许您在单个图表中表示不同的变量。
• 您可以快速比较不同变量的值。

缺点：

• 有时可能很难知道确切的值。
• 很难表示数值范围差异很大的变量。
• 如果放射状图表中表示了许多变量，则可能存在太多轴，因此图表将更难以阅读。
• 很少有数据系列可以用放射状图表表示，因为如果多边形重叠，则很难理解图表。
• 只有定量数据才能在蜘蛛图中表示。