集合运算:并、交、补、差
集合是元素的集合。
我们用大写字母指定一个集合,并使用花括号定义该集合的元素。例如,假设我们有一个名为“A”的集合,其中包含元素 1、2、3。我们可以将其写如下:
A = {1, 2, 3}
本教程解释了概率和统计中最常用的集合运算。
联盟
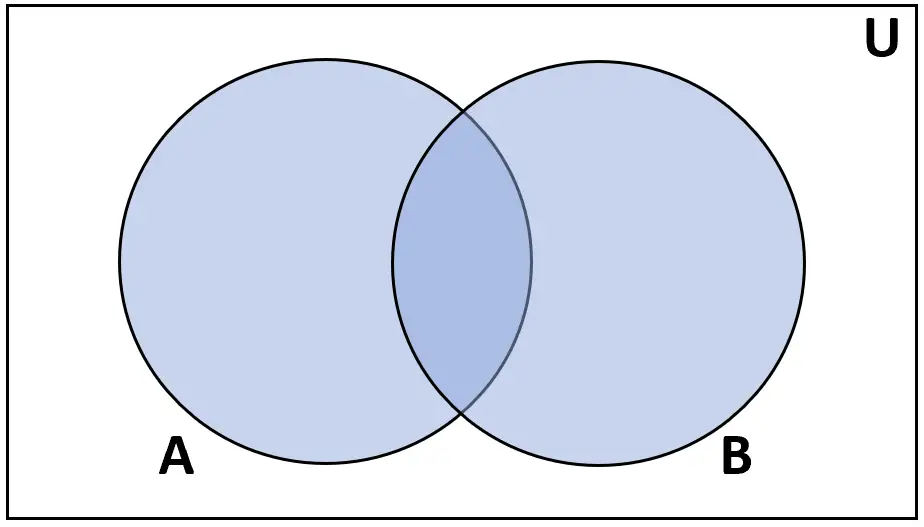
定义:集合A 和 B 的并集是在 A 或 B 中找到的元素的集合。
评级: A∪B
例子:
- {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
- {1, 2} ∪ {1, 2} = {1, 2}
- {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}
路口
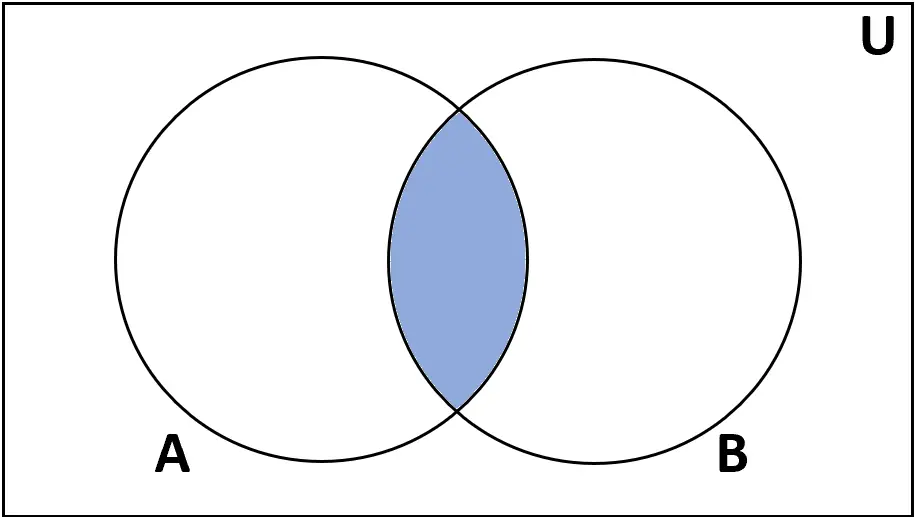
定义:集合A和B的交集是在A和B中都找到的元素的集合。
符号: A∩B
例子:
- {1, 2, 3} ∩ {4, 5, 6} = {∅}
- {1, 2} ∩ {1, 2} = {1, 2}
- {1, 2, 3} ∩ {3, 4} = {3}
补充
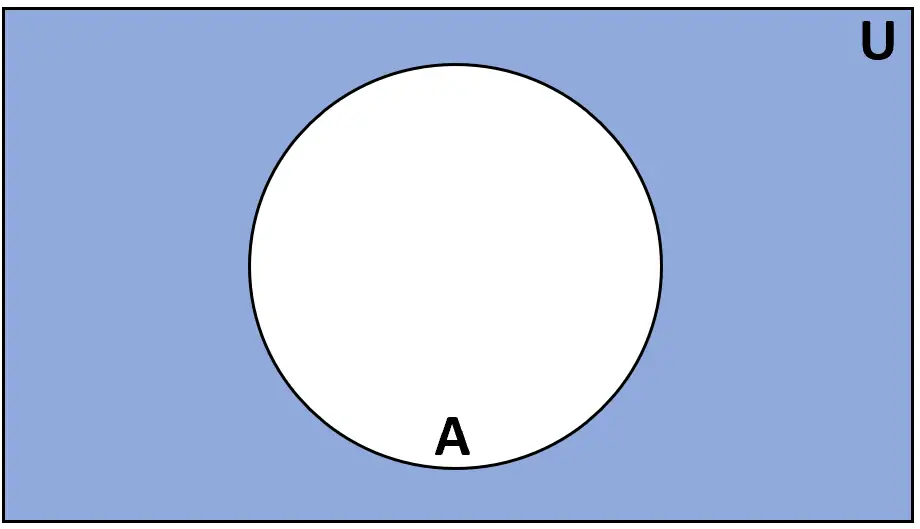
定义:集合A的补集是在全集U中但不在A中的元素的集合。
评级: A’ 或Ac
例子:
- 如果 U = {1, 2, 3, 4, 5, 6} 且 A = {1, 2},则 A c = {3, 4, 5, 6}
- 如果 U = {1, 2, 3} 且 A = {1, 2},则 A c = {3}
不同之处
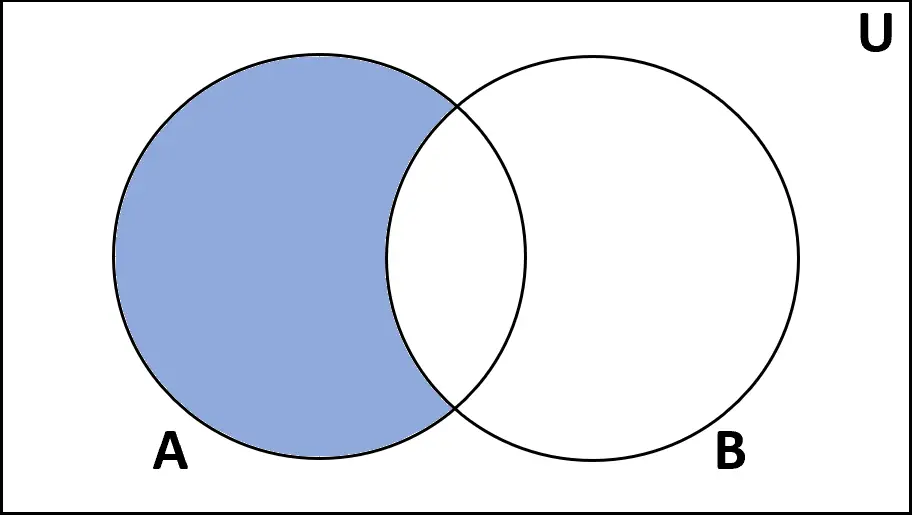
定义:集合A和B之间的差异是在A中找到但在B中没有找到的元素的集合。
评级: A-B
例子:
- {1,2,3} – {2,3,4} = {1}
- {1, 2} – {1, 2} = {∅}
- {1, 2, 3} – {4, 5} = {1, 2, 3}
对称差
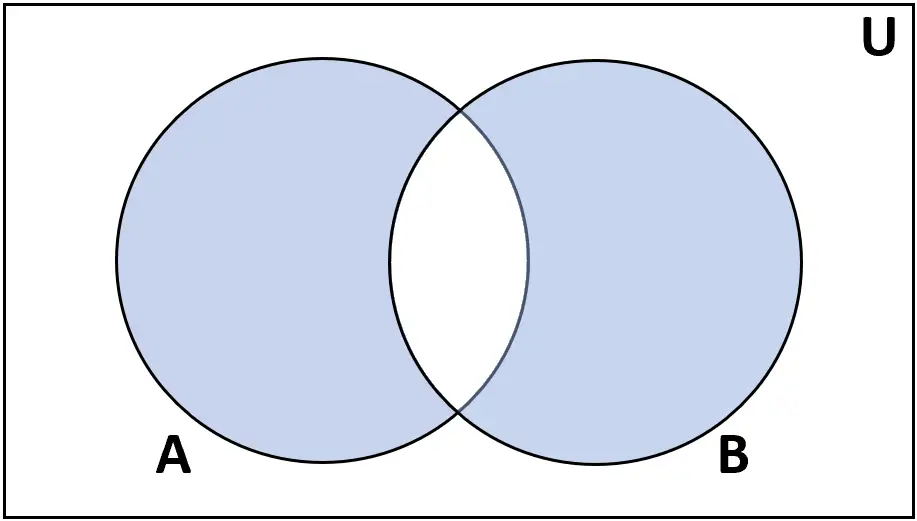
定义:集合 A 和 B 的对称差是在 A 或 B 中找到的元素的集合,但不能在两者中找到。
评级: AΔB
例子:
- {1, 2, 3} Δ {2, 3, 4} = {1, 4}
- {1, 2} Δ {1, 2} = {∅}
- {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}
笛卡尔积
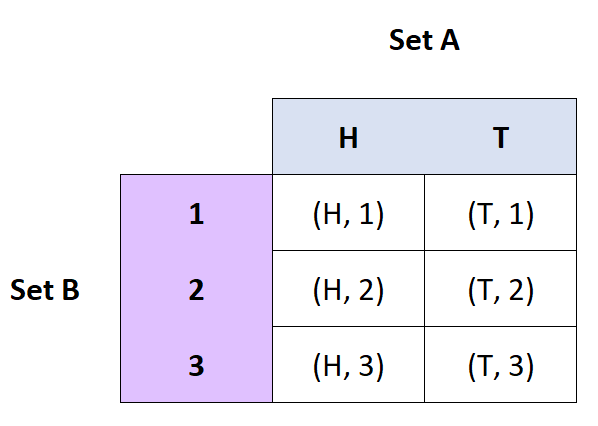
定义:集合 A 和 B 的笛卡尔积是 A 和 B 的有序对的集合。
评级: A×B
例子:
- 如果 A = {H, T} 且 B = {1, 2, 3},则 A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( T, 2), (T, 3)}
- 如果 A = {T, H} 且 B = {1, 2, 3},则 A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( H, 2), (H, 3)}