斯特奇斯法则
本文解释了什么是斯特奇斯规则及其公式。您还将找到斯特奇规则的分步具体示例,以及在线斯特奇规则计算器。
斯特奇斯法则是什么?
斯特吉斯规则是用于计算数据集应划分的理想类数或区间数的规则。
斯特吉斯规则的公式指出,类的数量等于一加上数据总数的以 2 为底的对数。
![]()
金子
![]()
是班级或间隔的数量,
![]()
是样本中观测值的总数。
大多数计算器只允许以 10 为底的对数进行计算。在这种情况下,您可以使用以下等效公式:
![]()
斯特奇规则是由德国统计学家赫伯特·斯特奇于 1926 年创建的。
斯特吉斯规则的示例
现在我们知道了斯特奇斯规则是什么,我们将通过解决逐步练习来了解如何使用统计中的斯特奇斯规则来计算数据集的间隔。
- 测量了50个不同人的样本量,所有值都记录在下面的数据表中。应用斯特吉斯规则将数据集划分为多个区间,然后将数据绘制在直方图上。

首先,我们需要将数据分成区间。总共有 50 个数据元素,因此我们使用 Sturges 规则与此值:
![Rendered by QuickLaTeX.com \begin{array}{l}c=1+\log_2(N)\\[2ex]c=1+\log_2(50)\\[2ex]c=1+5,64\\[2ex]c=6,64\\[2ex]c\approx 7\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-9929b0c8f1f7cdf5a6160c07e0205c46_l3.png)
因此,有必要将数据分开并将它们分为七个区间。我们现在需要知道每个区间的宽度,为此,只需将最大值减去最小值除以区间总数:
![]()
简而言之,振幅为9的区间必须有7个,因此使用Sturges方法计算出的区间为:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
计算完区间后,我们需要统计某个数据在每个区间出现的次数,并构建频数表:
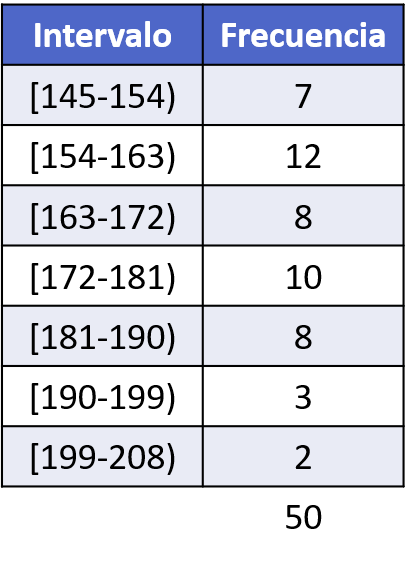
最后,从频率表中,我们可以创建直方图来绘制数据:
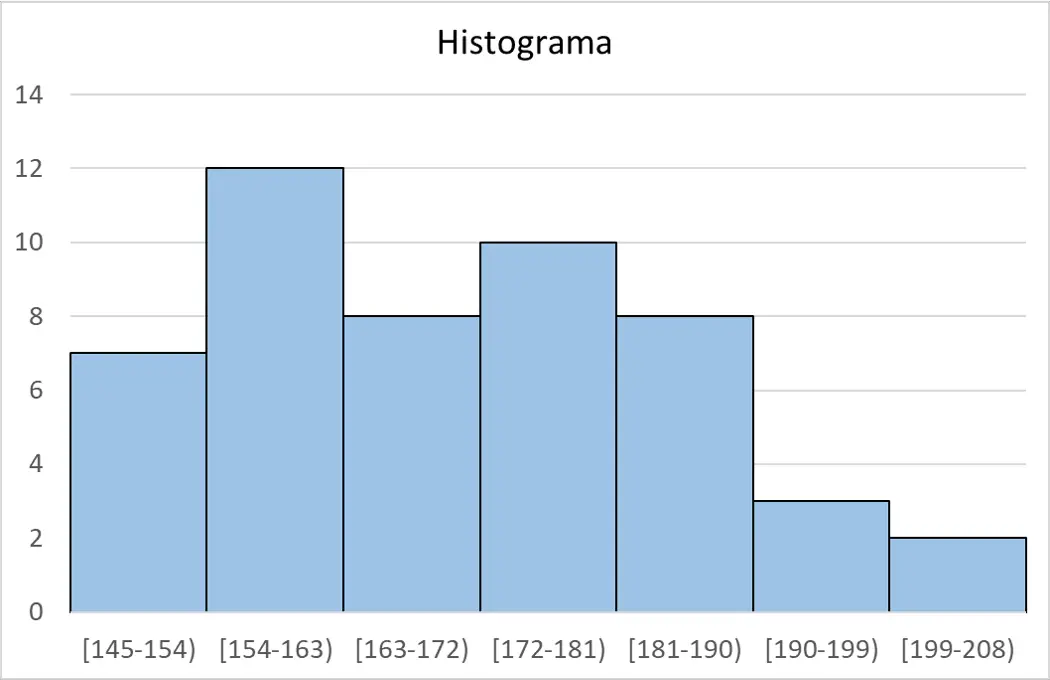
➤请参阅:如何制作直方图
斯特奇斯规则计算器
输入数据样本总数,点击“计算”,计算器将返回根据Sturges规则计算出的区间数。