如何在 spss 中执行多元方差分析

单向方差分析用于确定解释变量的不同水平是否会导致某些响应变量出现统计上不同的结果。

例如，我们可能有兴趣了解三个教育级别（副学士学位、学士学位、硕士学位）是否会导致年收入在统计上有所不同。在这种情况下，我们有一个解释变量和一个响应变量。

• 解释变量：教育水平
• 响应变量：年收入

多元方差分析是单向方差分析的扩展，其中有多个响应变量。例如，我们可能有兴趣了解教育水平是否会导致不同的年收入和不同数量的学生债务。在这种情况下，我们有一个解释变量和两个响应变量：

• 解释变量：教育水平
• 响应变量：年收入、学生债务

由于我们有多个响应变量，因此在这种情况下使用多元方差分析是合适的。

在本教程中，我们将解释如何在 SPSS 中执行多元方差分析。

示例：SPSS 中的多元方差分析

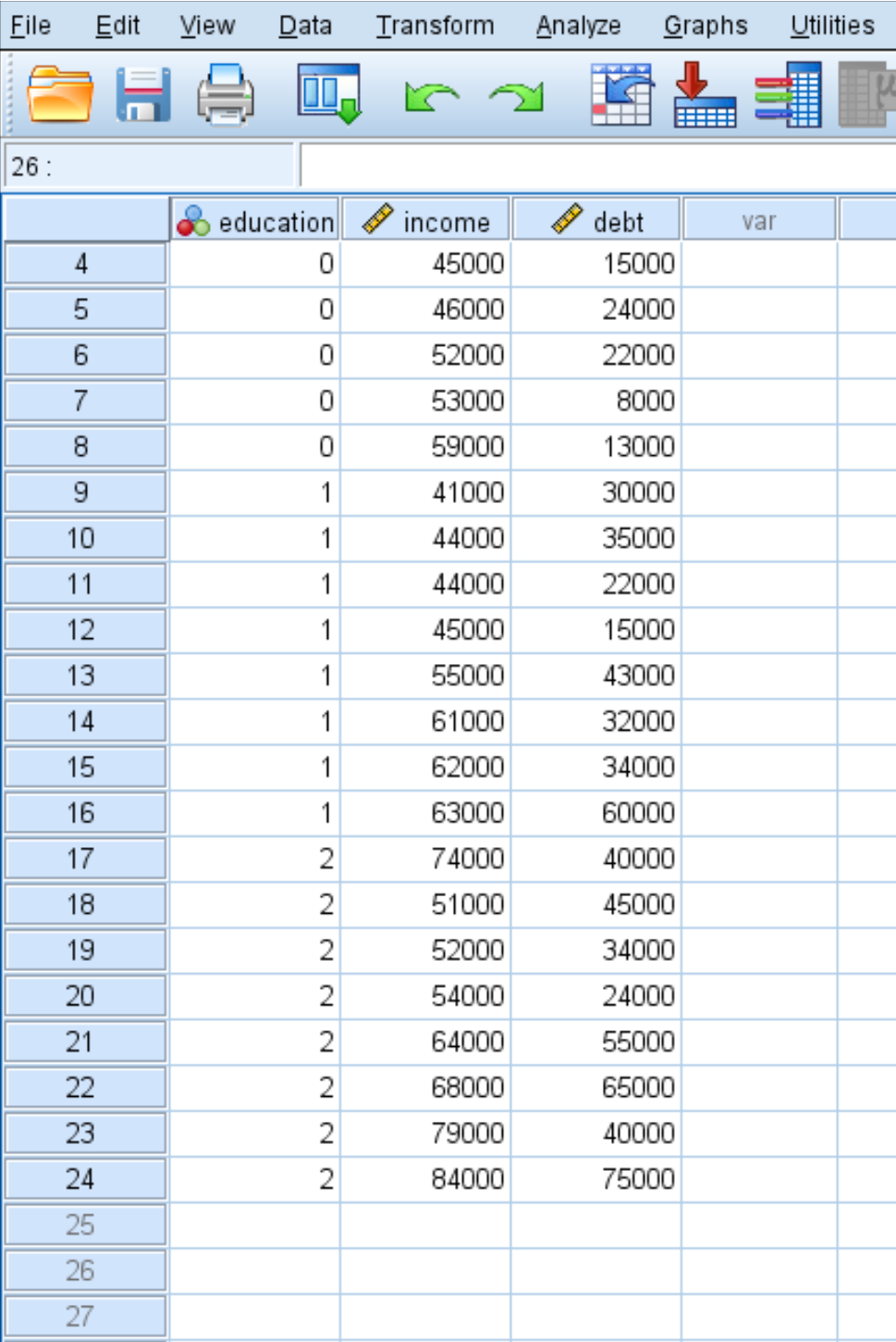
为了说明如何在 SPSS 中执行多元方差分析，我们将使用以下数据集，其中包含 24 人的以下三个变量：

• educ：学习水平（0 = 副学士学位，1 = 学士，2 = 硕士）
• 收入：年收入
• 债务：学生贷款债务总额

使用以下步骤在 SPSS 中执行多元方差分析：

步骤 1：执行多元方差分析。

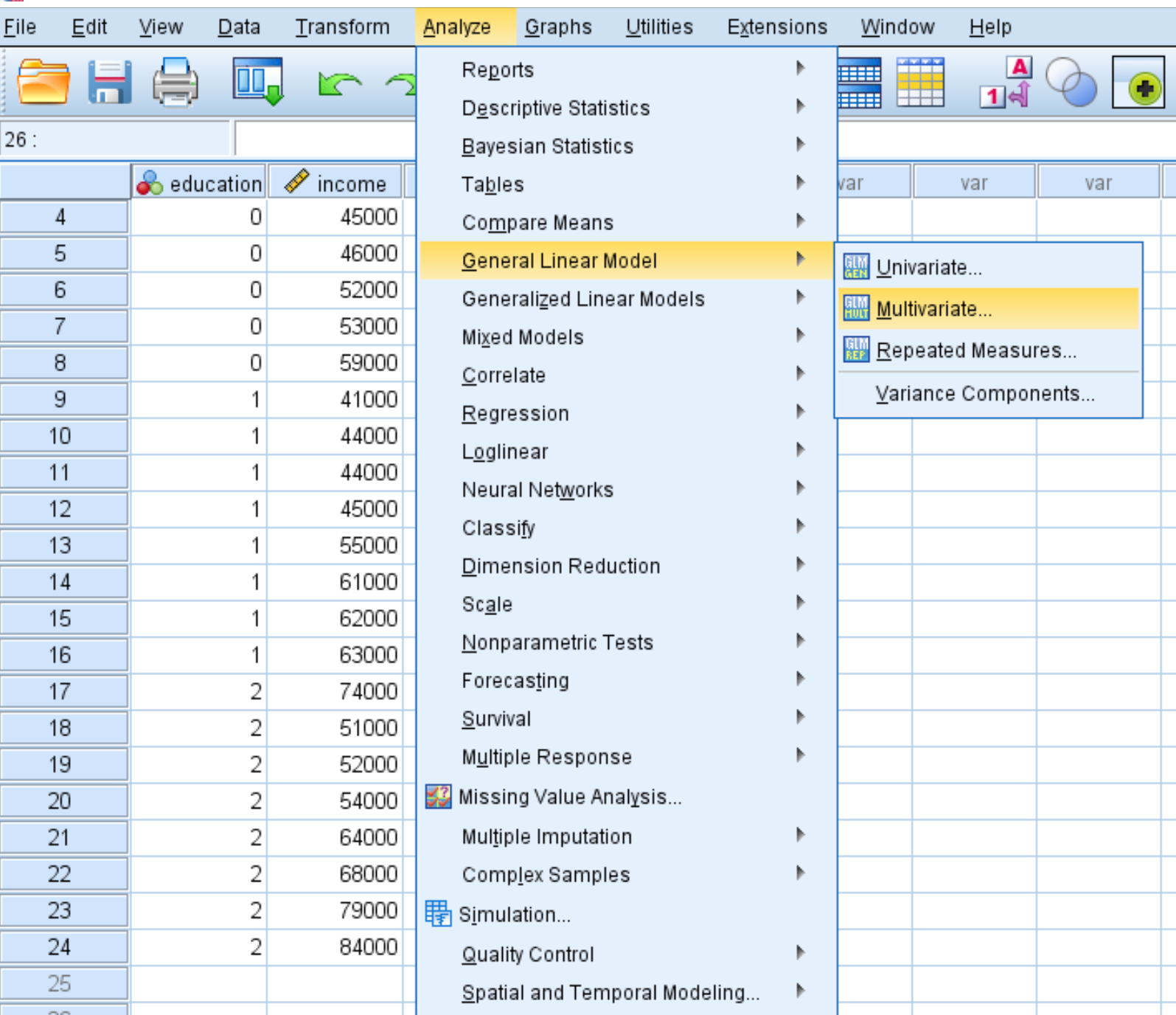
单击“分析”选项卡，然后单击“一般线性模型” ，然后单击“多元” ：

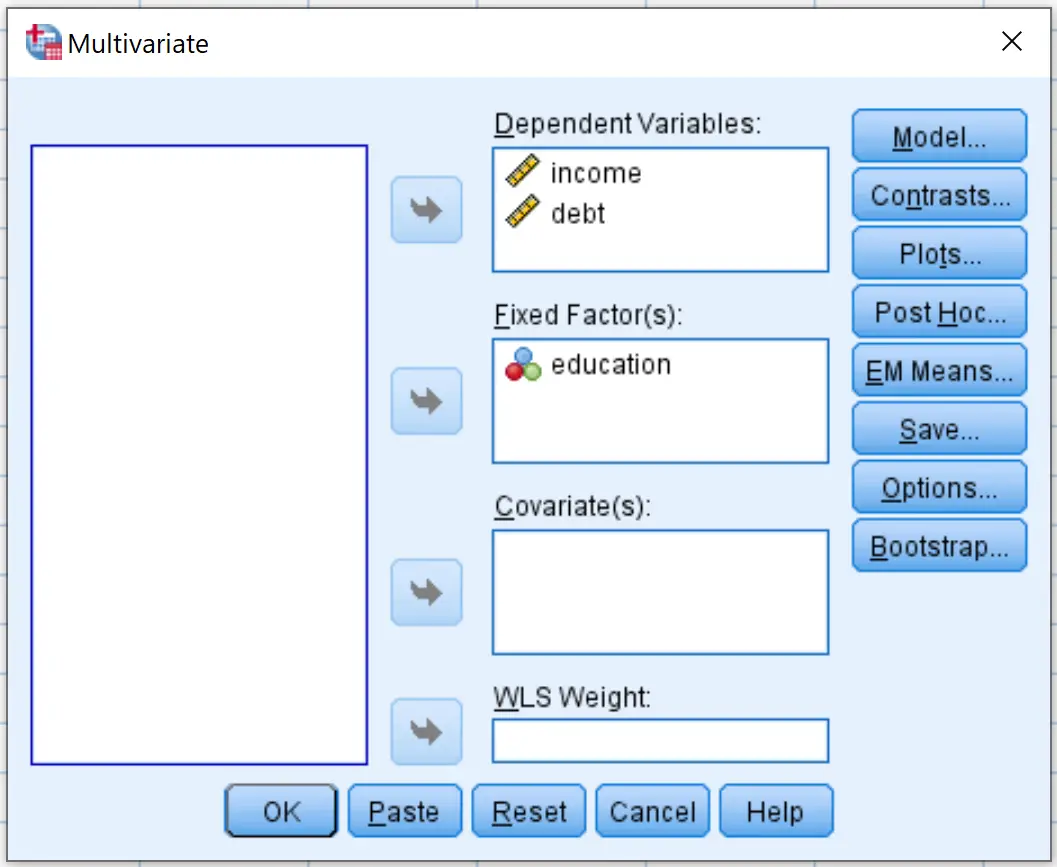
在出现的新窗口中，将收入和债务变量拖到标有“因变量”的框中。然后将教育因素变量拖到标记为固定因素的框中：

接下来，单击事后按钮。将教育因素拖到标有事后测试的框中。然后选中Tukey旁边的框。然后单击“继续” 。

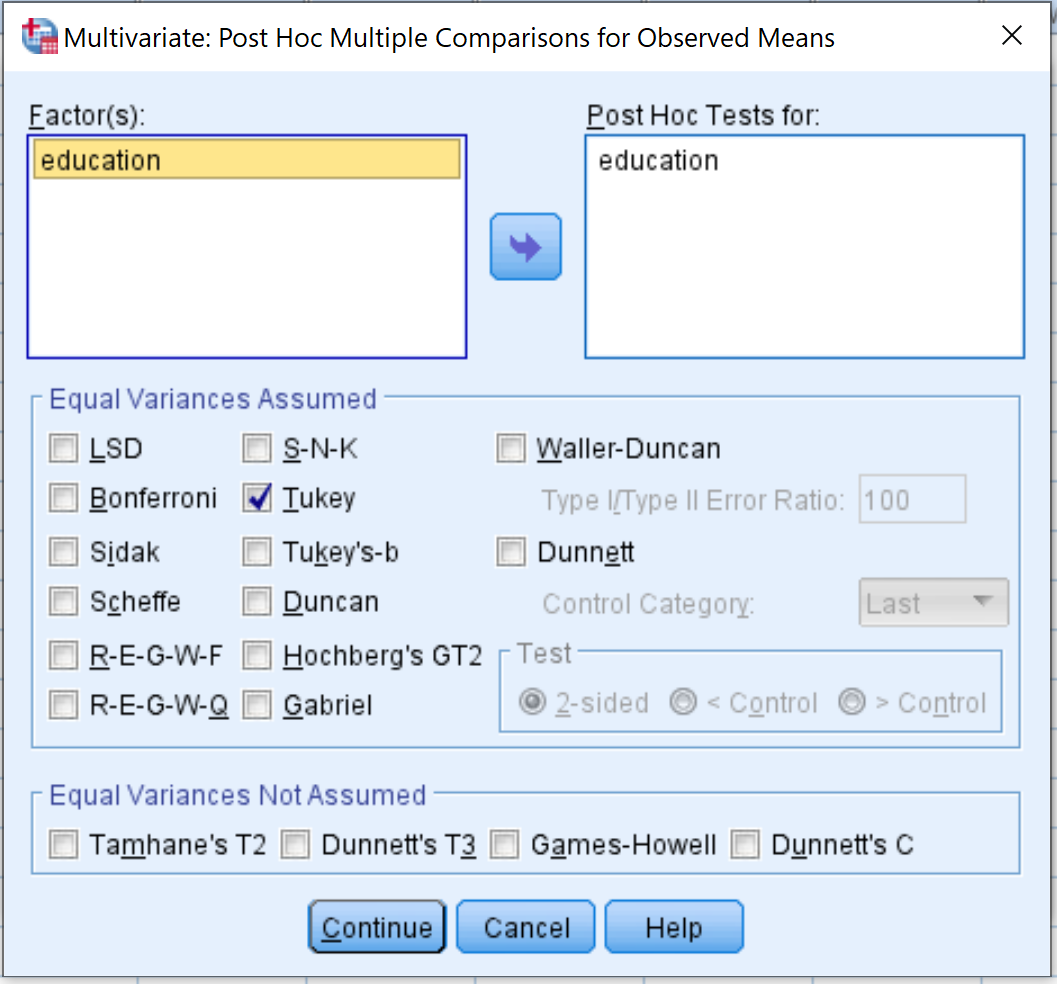
最后，单击“确定” 。

第 2 步：解释结果。

单击“确定”后，将显示多元方差分析结果。以下是如何解释结果：

多变量测试

该表告诉您教育程度是否会导致年收入和学生债务总额存在统计上的显着差异。我们将查看标记为Wilks’ Lambda的行中的数字：

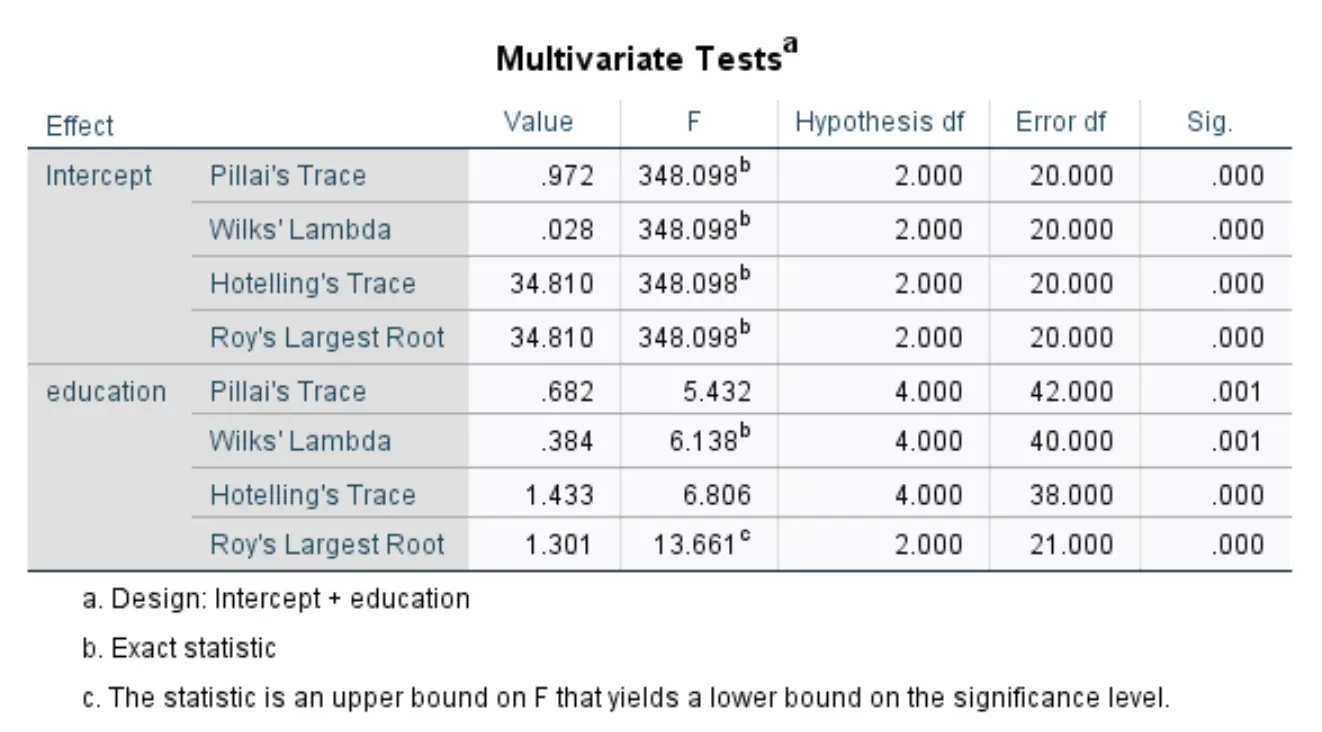
总体 F 统计量为6.138 ，相应的 p 值为0.001 。由于该值小于0.05，这表明教育水平对年收入和学生债务总额有显着影响。

受试者间效应测试

该表显示了收入和债务的个人 p 值：

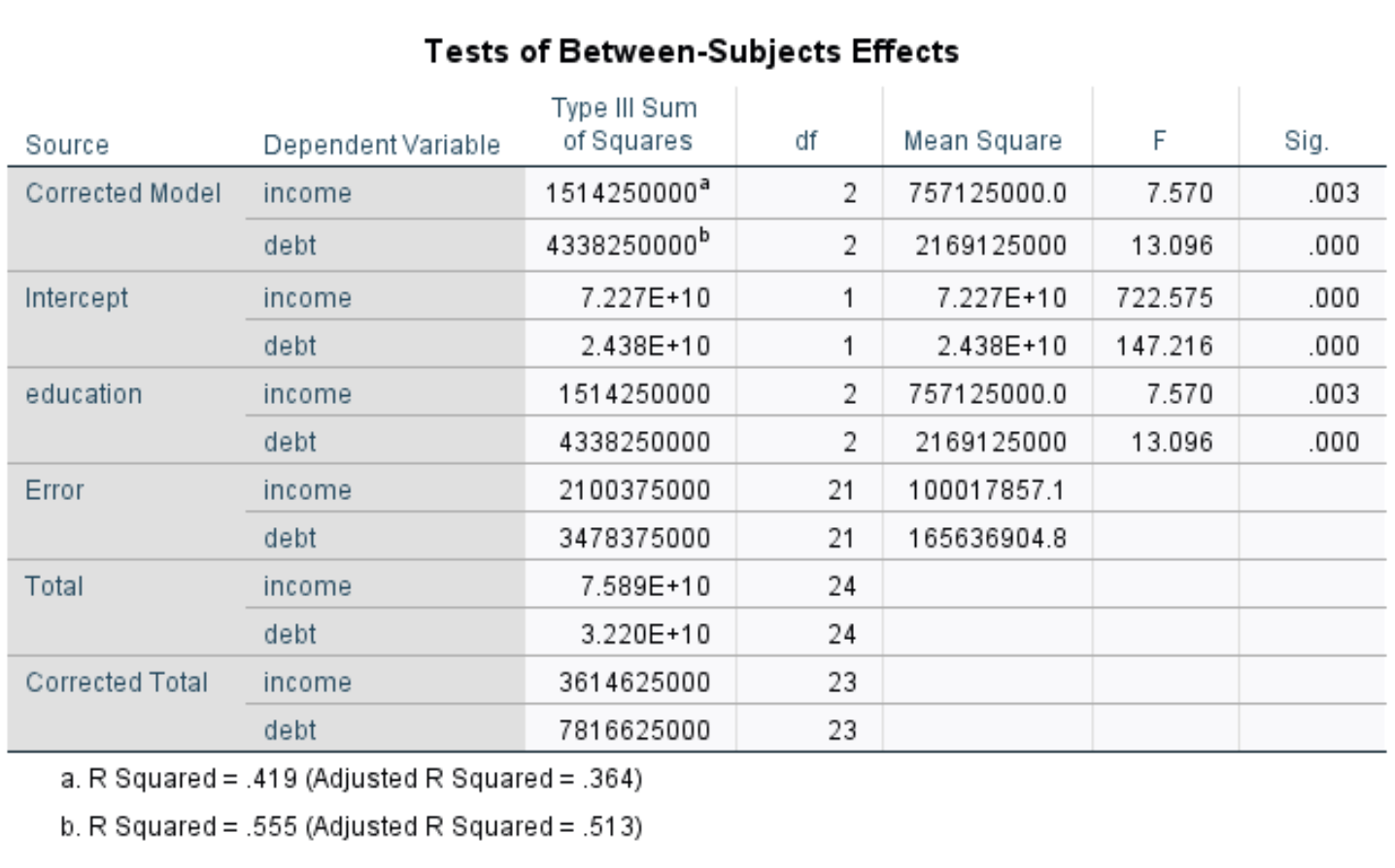
收入的 p 值为0.003 ，债务的 p 值为0.000 。由于这两个值都小于0.05，这意味着教育水平对收入和债务有统计上显着的影响。

事后测试

该表显示了图基对每个教育级别的事后比较。

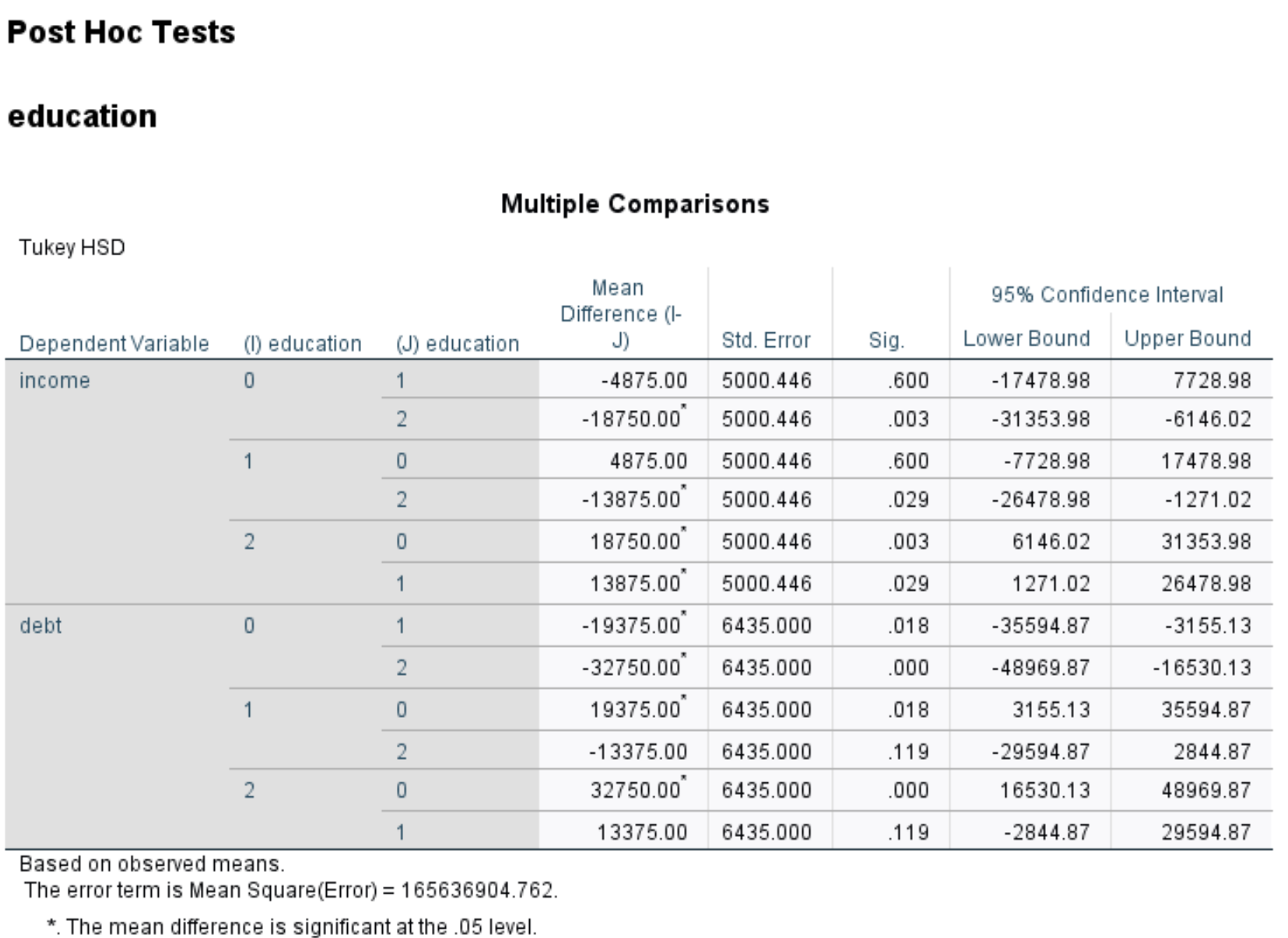
从表中我们可以观察到以下几点：

• 拥有副学士学位（教育= 0）的人的收入与拥有硕士学位（教育= 1）的人的收入存在显着差异| p 值 = 0.003 。
• 拥有学士学位（学历=1）的人的收入数额与拥有硕士学位（学历=2）的人的收入数额存在显着差异| p 值 = 0.029 。
• 拥有副学士学位（教育= 0）的人的收入与拥有学士学位（教育= 1）的人的收入存在显着差异| p 值 = 0.018 。
• 拥有副学士学位（教育= 0）的人的收入与拥有硕士学位（教育= 2）的人的收入存在显着差异| p 值 = 0.000 。

进一步阅读： ANOVA、ANCOVA、MANOVA 和 MANCOVA 之间的区别