如何对不等样本量进行方差分析

当谈到统计时，学生经常问的一个问题是：

当每组样本量不相等时是否可以进行单向方差分析？

简短的回答：

是的，当样本量不相等时，您可以执行单向方差分析。相等的样本量不是方差分析中做出的假设之一。

然而，在样本量不等的情况下执行单向方差分析时，需要考虑两个潜在问题：

(1)统计功效降低。

(2)稳健性降低为方差不等。

以下各节详细解释了这两个潜在问题。

问题#1：统计功效降低

当我们使用任何类型的统计检验来比较组时，当每个组具有相同的样本量时，检验的统计功效最高。

回想一下，统计功效是指测试检测到实际存在效果的概率。

可以看出，组间样本量差异越大，方差分析的统计功效越低。

这就是为什么研究人员通常希望样本量相同，以获得更高的功效，从而更有可能检测到真正的差异。

当然可以使用不等的样本量执行单向方差分析，但您应该意识到单向方差分析的功效将会降低。

问题#2：稳健性降低为方差不等

单向方差分析的假设之一是每组之间的方差相等。

一般来说，单向方差分析被认为对于违反等方差假设是稳健的，但前提是每个组具有相同的样本量。

因此，如果样本量不相等并且组之间的方差也不相等，那么单向方差分析的结果可能难以信任。

如何决定是否使用样本量不等的单向方差分析

如果您的样本量不相等，并且想要执行单向方差分析来测试组均值之间的差异，您可以使用以下流程图来决定如何继续：

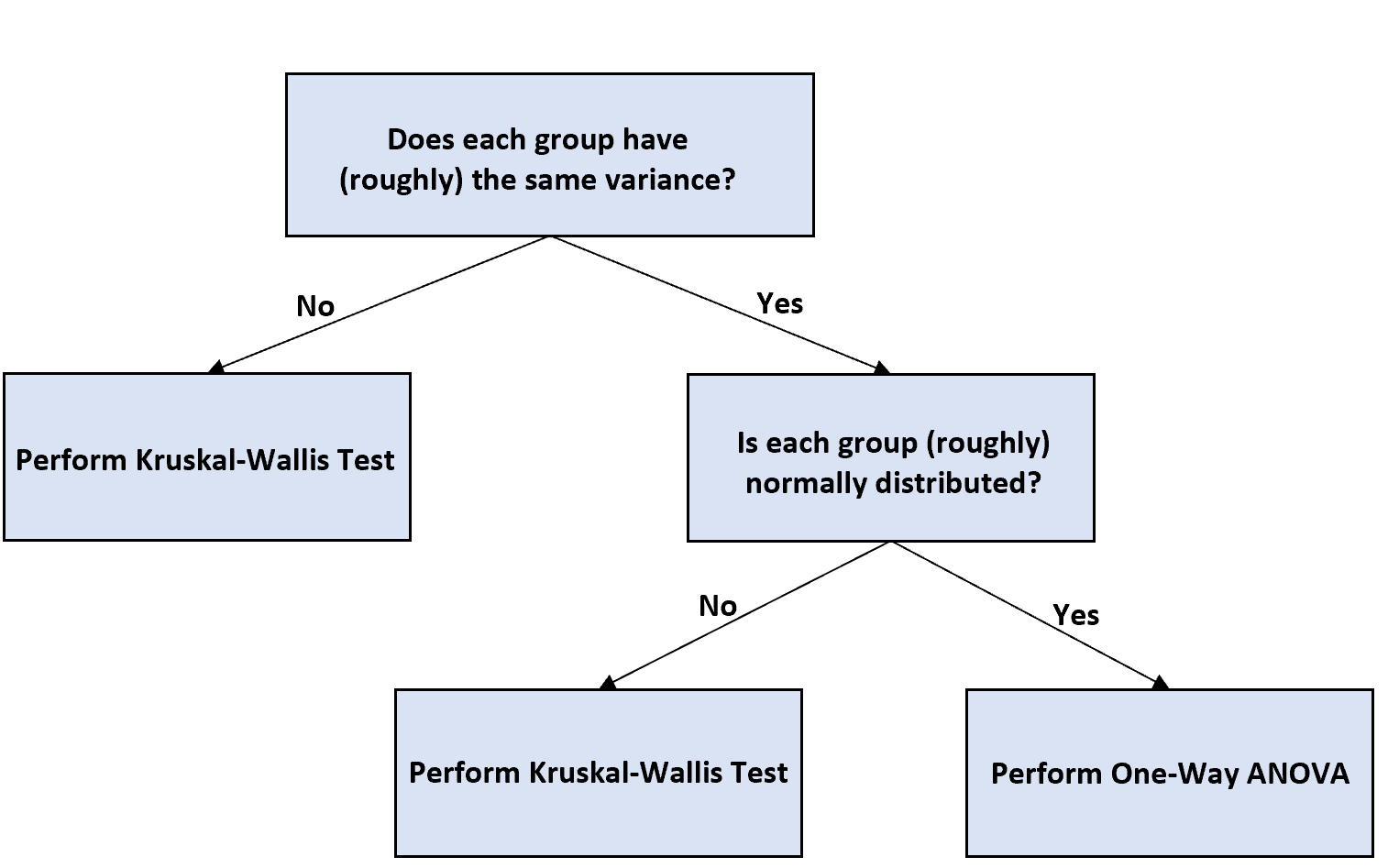
下面简单解释一下流程图：

步骤1：确定每个组是否具有相同的方差。

要确定每个组是否具有相同的方差，您可以使用以下两种方法之一：

• 为每个组创建箱线图，并查看每个组中值的分布是否近似相等。
• 对等方差执行正式的统计检验，例如Bartlett 检验。

如果方差不相等，则执行Kruskal-Wallis 检验，该检验被认为是单向方差分析的非参数等效项。

如果间隙相等，则继续下一步。

步骤2：判断各组是否服从正态分布。

要确定每组中的值是否近似正态分布，可以使用以下两种方法之一：

• 为每个组创建直方图或QQ 图。
• 执行正式的统计检验，例如 Shapiro-Wilk、Kolmogorov-Smironov、Jarque-Barre 或 D’Agostino-Pearson。

如果每个组呈正态分布，您可以进行单向方差分析并像解释任何普通单向方差分析一样解释结果。

如果每个组不是正态分布，则执行 Kruskal-Wallis 检验。

其他资源

单向方差分析简介
如何检查方差分析假设
克鲁斯卡尔-沃利斯检验简介
如何解释方差分析中的F值和P值