了解方差分析模型的原假设

单向方差分析用于确定三个或更多独立组的平均值之间是否存在统计显着性差异。

单向方差分析使用以下原假设和备择假设：

• H ₀ : μ ₁ = μ ₂ = μ ₃ = … = μ _k （所有组均值相等）
• H _A :至少一组平均值不同 休息

为了决定是否应该拒绝原假设，我们需要参考方差分析表结果中的 p 值。

如果 p 值低于一定的显着性水平（例如 0.05），那么我们可以拒绝原假设并得出并非所有组均值都相等的结论。

双向方差分析用于确定分配给两个变量（有时称为“因子”）的三个或更多独立组的平均值之间是否存在统计显着差异。

双向方差分析同时检验三个零假设：

• 所有组均值在第一个变量的每个水平上都相等
• 所有组均值在第二个变量的每个水平上都相等
• 两个变量之间不存在交互作用

为了决定是否应该拒绝每个原假设，我们需要参考双向方差分析表结果中的 p 值。

以下示例显示如何决定是否拒绝单向方差分析和双向方差分析中的原假设。

示例 1：单向方差分析

假设我们想知道三种不同的考试准备计划是否会导致给定考试的平均分数不同。为了测试这一点，我们招募了 30 名学生参加一项研究，并将他们分为三组。

每组的学生被随机分配在接下来的三周内使用三个考试准备计划之一来准备考试。三周结束时，所有学生都参加相同的考试。

各组考试成绩如下：

当我们将这些值输入单向方差分析计算器时，我们会收到以下方差分析表作为输出：

请注意，p 值为0.11385 。

对于这个特定的例子，我们将使用以下原假设和备择假设：

• H ₀ : μ ₁ = μ ₂ = μ ₃ (各组平均考试成绩相等)
• H _A :至少一组平均值不同 休息

由于方差分析表的 p 值不小于 0.05，因此我们无法拒绝原假设。

这意味着我们没有足够的证据表明三组的平均考试成绩之间存在统计上的显着差异。

示例 2：双向方差分析

假设植物学家想知道植物生长是否受到阳光照射和浇水频率的影响。

她种下了 40 颗种子，让它们在不同的阳光照射和浇水频率条件下生长两个月。两个月后，她记录了每株植物的高度。结果如下所示：

在上表中，我们看到每种条件组合下都生长了五株植物。

例如，每天浇水且没有阳光的情况下种植五株植物，两个月后它们的高度分别为 4.8 英寸、4.4 英寸、3.2 英寸、3.9 英寸和 4.4 英寸：

她在 Excel 中执行双向方差分析并获得以下结果：

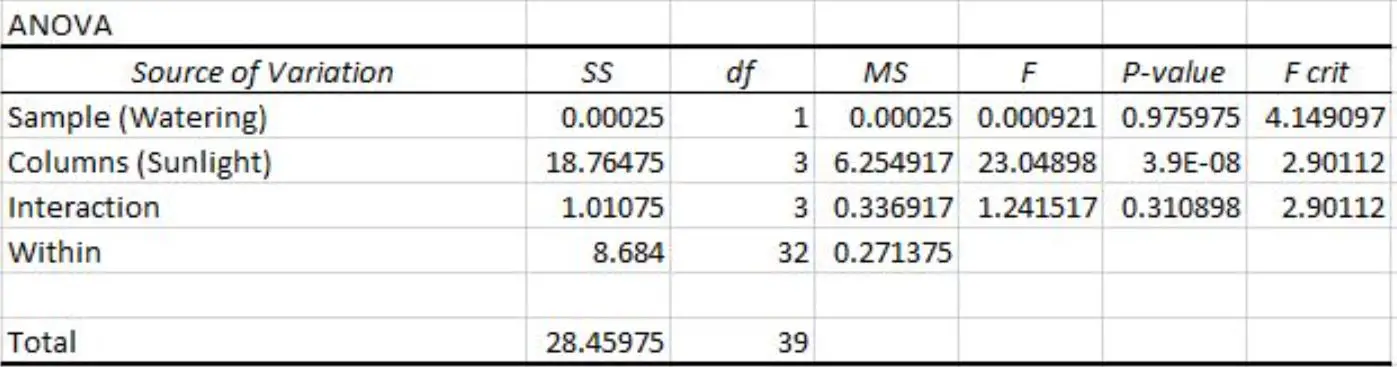
我们可以在双向方差分析表结果中看到以下p值：

• 浇水频率的 p 值为0.975975 。这在 0.05 显着性水平上不具有统计显着性。
• 阳光照射的 p 值为3.9E-8 (0.000000039) 。这在 0.05 显着性水平上具有统计显着性。
• 浇水频率和阳光照射之间相互作用的 p 值为0.310898 。这在 0.05 显着性水平上不具有统计显着性。

这些结果表明，阳光照射是对植物高度具有统计显着影响的唯一因素。

而且由于不存在交互作用，因此阳光照射的效果在每个浇水频率水平上都是一致的。

简而言之，植物每天还是每周浇水对于阳光照射对植物的影响没有影响。

其他资源

以下教程提供有关 ANOVA 模型的其他信息：

如何解释方差分析中的F值和P值
如何计算方差分析中的平方和
方差分析中高 F 值意味着什么？