方差可以为负吗？

在统计学中，术语方差是指给定数据集中的值如何分布。

学生提出的关于方差的一个常见问题是：

方差可以为负吗？

答案：不，方差不能为负。它可以取的最低值是零。

要理解为什么会出现这种情况，我们需要了解方差的实际计算方式。

如何计算间隙

求样本方差（表示为s ² ）的公式为：

s ² = Σ ( _xi – x ) ² / (n-1)

金子：

• x ：样本平均值
• x _i ：样本中的^{第 i 个}观察值
• N ：样本量
• Σ ：希腊符号，意思是“和”

例如，假设我们有以下包含 10 个值的数据集：

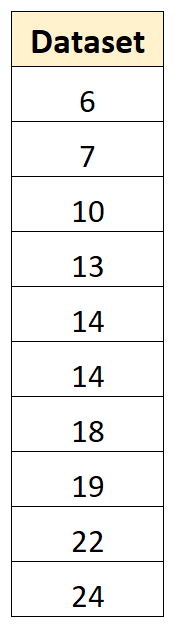
我们可以使用以下步骤来计算该样本的方差：

第 1 步：求平均值

平均数只是平均数。结果是14.7 。

第 2 步：求偏差平方

然后我们可以计算每个单独值与平均值的平方偏差。

例如，第一平方偏差计算为 (6-14.7) ² = 75.69。

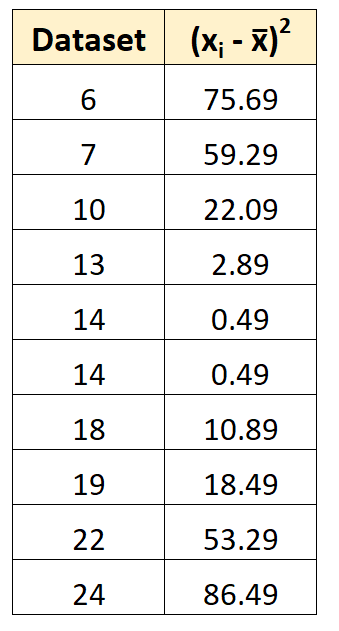
步骤 3：求偏差平方和

然后我们可以将所有偏差的平方相加：

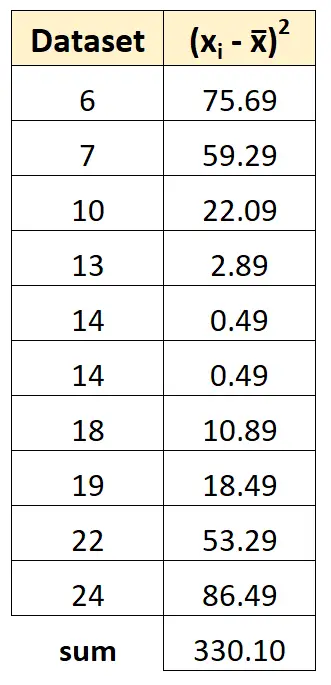
步骤 4：计算样本方差

最后，我们可以将样本方差计算为偏差平方和除以 (n-1)：

s ² = 330.1 / (10-1) = 330.1 / 9 = 36.678

样本方差结果为36,678 。

零方差的例子

数据集具有零方差的唯一方法是数据集中的所有值都相同。

例如，以下数据集的样本方差为零：

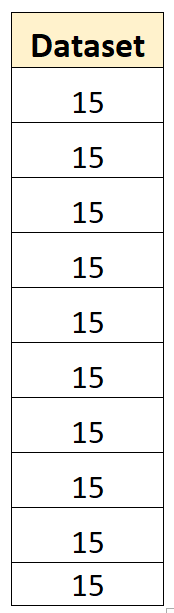
数据集的平均值为15，没有任何单个值偏离平均值。因此，偏差的平方和将为零，并且样本方差将为零。

标准差可以为负数吗？

衡量数据集中值的分布的更常见方法是使用标准差，即方差的平方根。

例如，如果给定样本的方差为^s2 = 36.678 ，则标准差（写作s ）计算如下：

s = √ ^s2 = √ 36.678 = 6.056

由于我们已经知道方差始终为零或正数，这意味着标准差永远不可能为负，因为零或正数的平方根不可能为负。

其他资源

集中趋势的度量：定义和示例
分散措施：定义和示例