什么是曲线回归? (定义和示例)
曲线回归是任何试图拟合曲线而不是直线的回归模型的名称。
曲线回归模型的常见示例包括:
二次回归:当预测变量和响应变量之间存在二次关系时使用。绘制图表时,这种类型的关系在散点图上看起来像“U”或倒“U”:
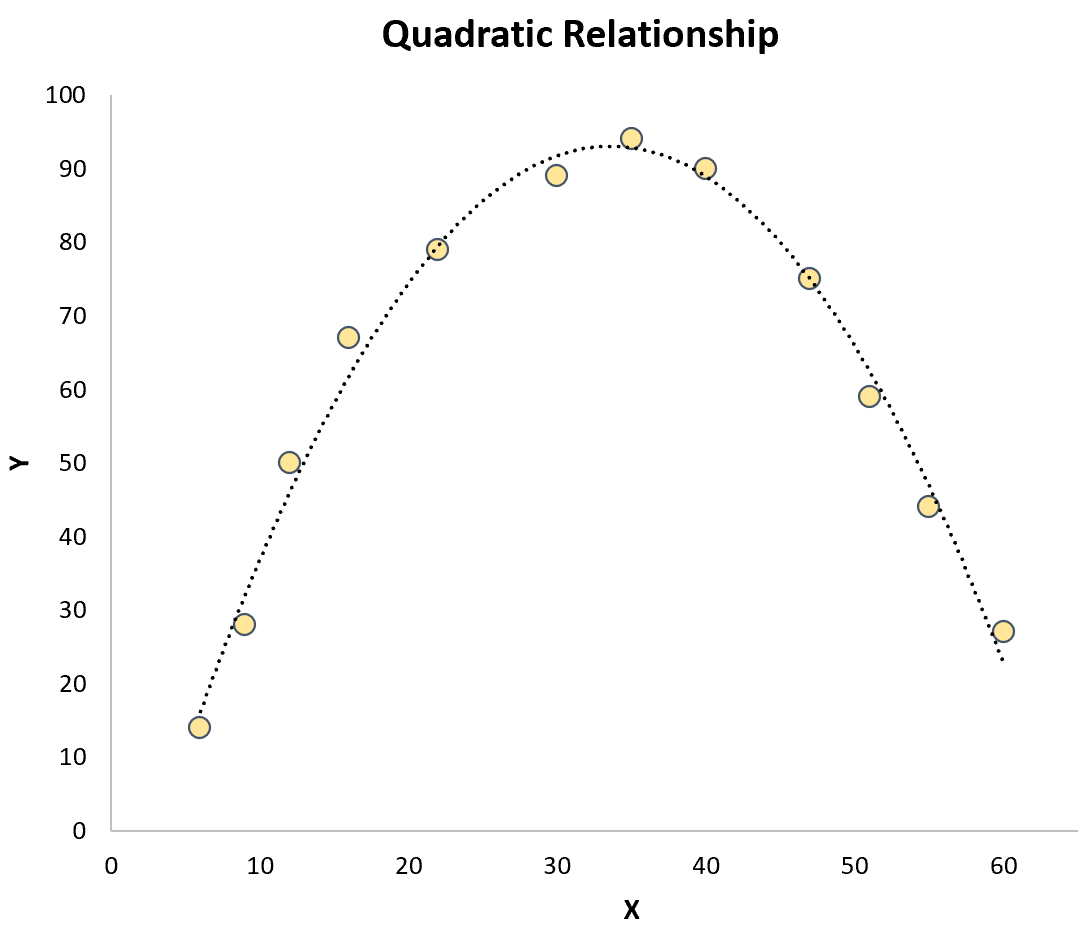
三次回归:当预测变量和响应变量之间存在三次关系时使用。绘制图表时,这种类型的关系在散点图上显示两条不同的曲线:
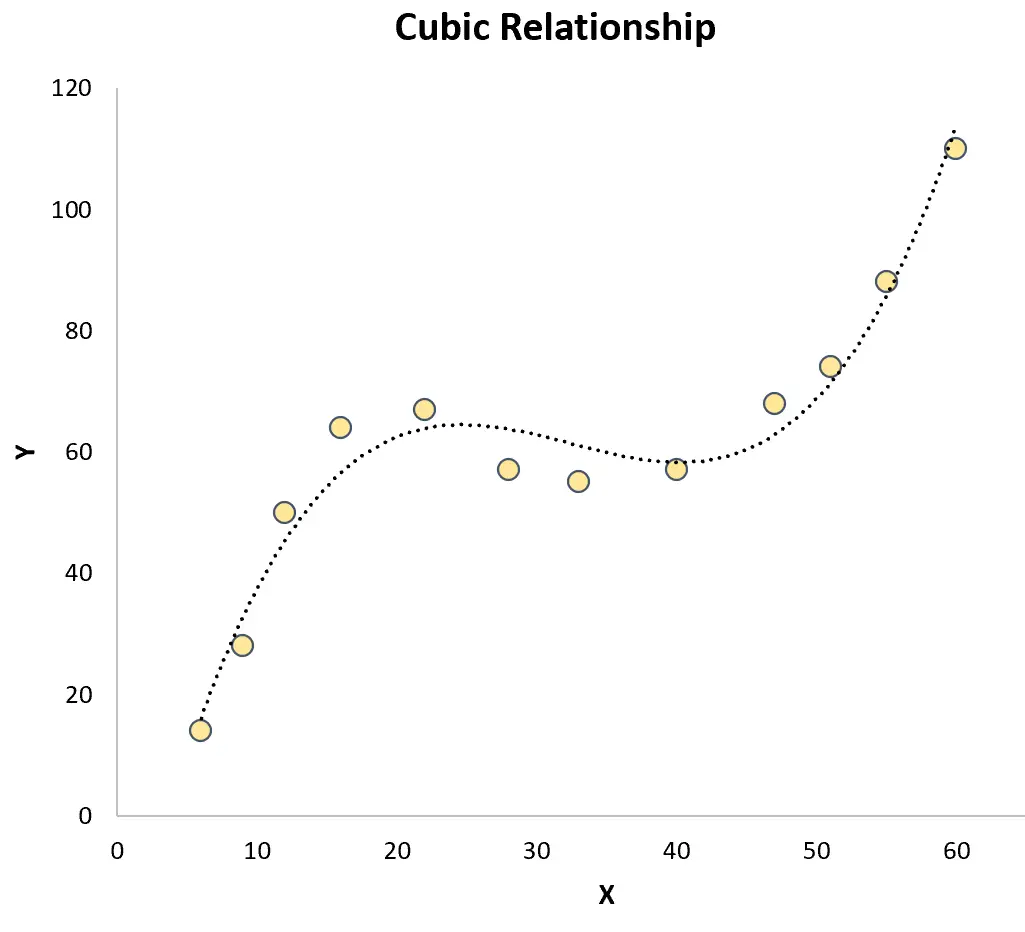
这两者都与简单线性回归形成对比,其中预测变量和响应变量之间的关系是线性的:
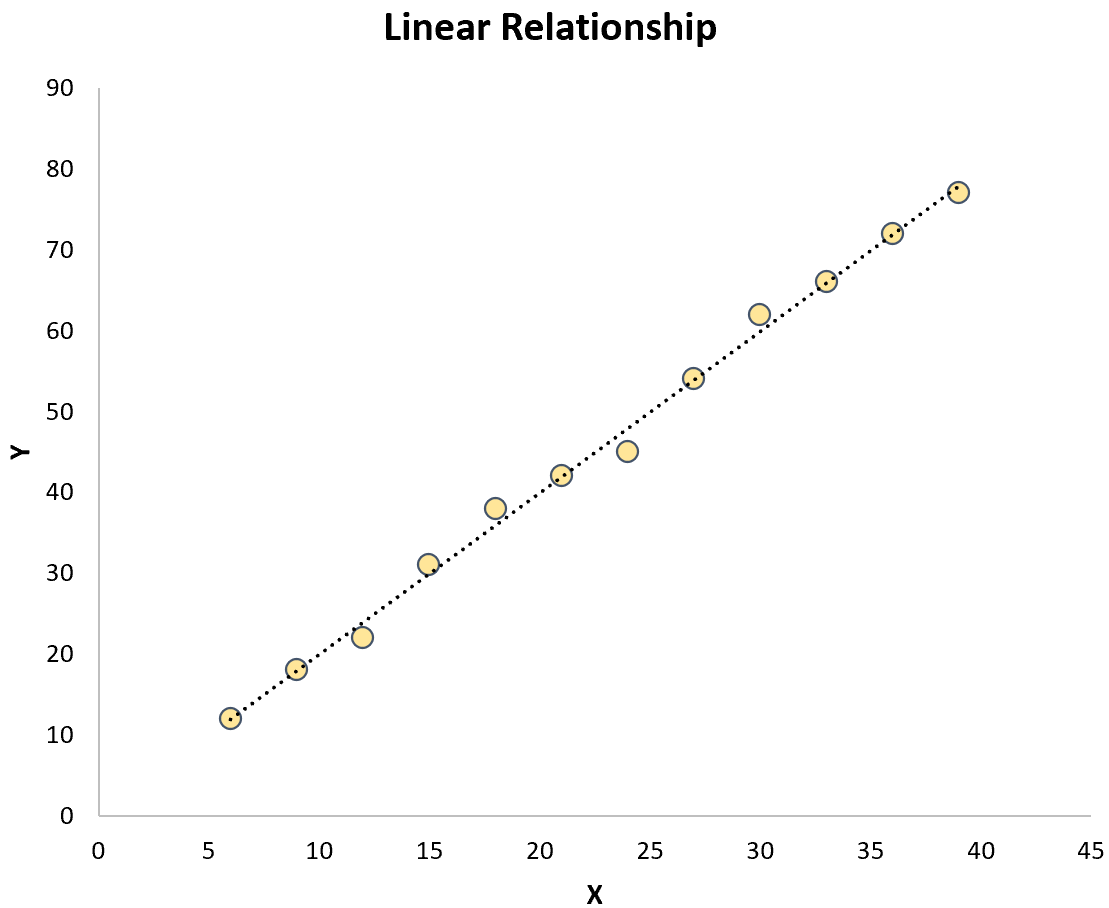
曲线回归模型的公式
简单的线性回归模型尝试使用以下公式拟合一组数据:
ŷ = β 0 + β 1 x
金子:
- ŷ:响应变量
- β 0 , β 1 :回归系数
- x:预测变量
相反,二次回归模型使用以下公式:
ŷ = β 0 + β 1 x + β 2 x 2
三次回归模型使用以下公式:
ŷ = β 0 + β 1 x + β 2 x 2 + β 3 x 3
包含指数的回归模型的更通用名称是多项式回归,它采用以下公式:
ŷ = β 0 + β 1 x + β 2 x 2 + … + β k x k
k的值表示多项式的次数。尽管次数可以是任何正数,但实际上我们很少拟合次数大于 3 或 4 的多项式回归模型。
通过在回归模型公式中使用指数,多项式回归模型能够将曲线而不是直线拟合到数据集。
何时使用曲线回归
了解是否应该使用曲线回归的最简单方法是创建预测变量和响应变量的散点图。
如果散点图显示两个变量之间存在线性关系,则简单的线性回归可能是合适的。
但是,如果散点图显示预测变量和响应变量之间存在二次、三次或其他曲线模式,则曲线回归可能更适合使用。
您还可以拟合一个简单的线性回归模型和一个曲线回归模型,并比较每个模型的拟合 R 平方值,以确定哪个模型提供了对数据的最佳拟合。
调整后的 R 平方非常有用,因为它告诉您响应变量中的方差有多少可以由预测变量解释,并根据模型中预测变量的数量进行调整。
一般来说,具有最高调整 R 平方值的模型可以更好地拟合数据集。
其他资源
以下教程解释了如何在不同的统计软件中执行多项式回归: