如何在 spss 中执行 mann-whitney u 检验
当样本分布不呈正态分布且样本量较小 (n < 30) 时, Mann -Whitney U 检验(有时称为 Wilcoxon 秩和检验)用于比较两个样本之间的差异。它被认为是双样本 t 检验的非参数等效项。
本教程介绍如何在 SPSS 中执行 Mann-Whitney U 检验。
示例:SPSS 中的 Mann-Whitney U 检验
研究人员想知道燃油处理是否会导致汽车平均英里/加仑的变化。为了测试这一点,他们进行了一项实验,测量了 12 辆经过燃油处理的汽车和 12 辆未经燃油处理的汽车的每加仑英里数。
以下屏幕截图显示了每辆车的 mpg 及其所属组(0 = 无燃油处理,1 = 燃油处理):
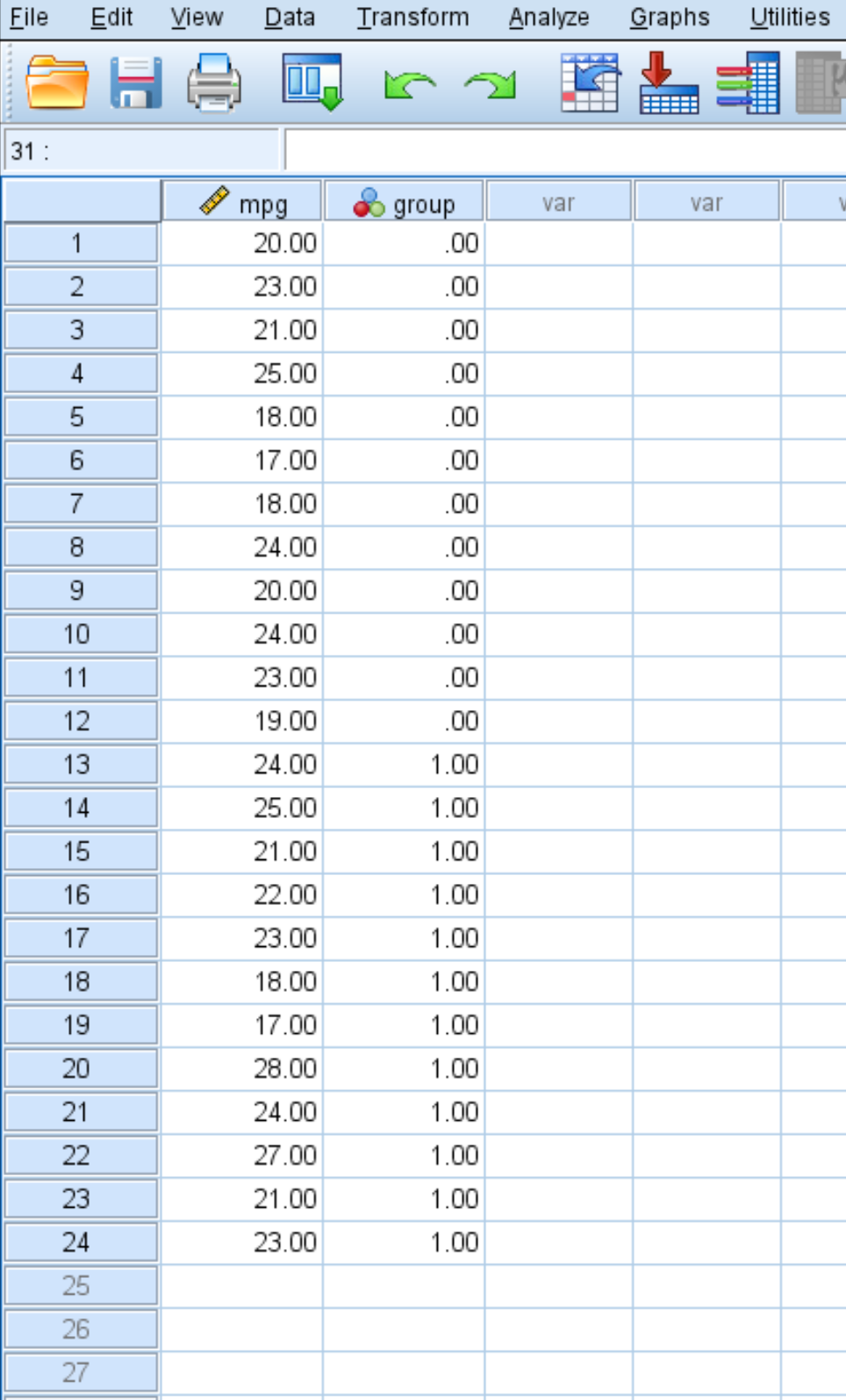
由于样本量很小,并且研究人员怀疑样本分布不是正态分布,因此他们决定进行 Mann-Whitney U 检验,以确定两组之间的 mpg 是否存在统计上的显着差异。
完成以下步骤以在 SPSS 中执行 Mann-Whitney U 检验。
步骤 1:选择 Mann-Whitney U 检验选项。
单击“分析”选项卡,然后单击“非参数检验”、 “旧版对话框” 、 “2 个独立样本” :
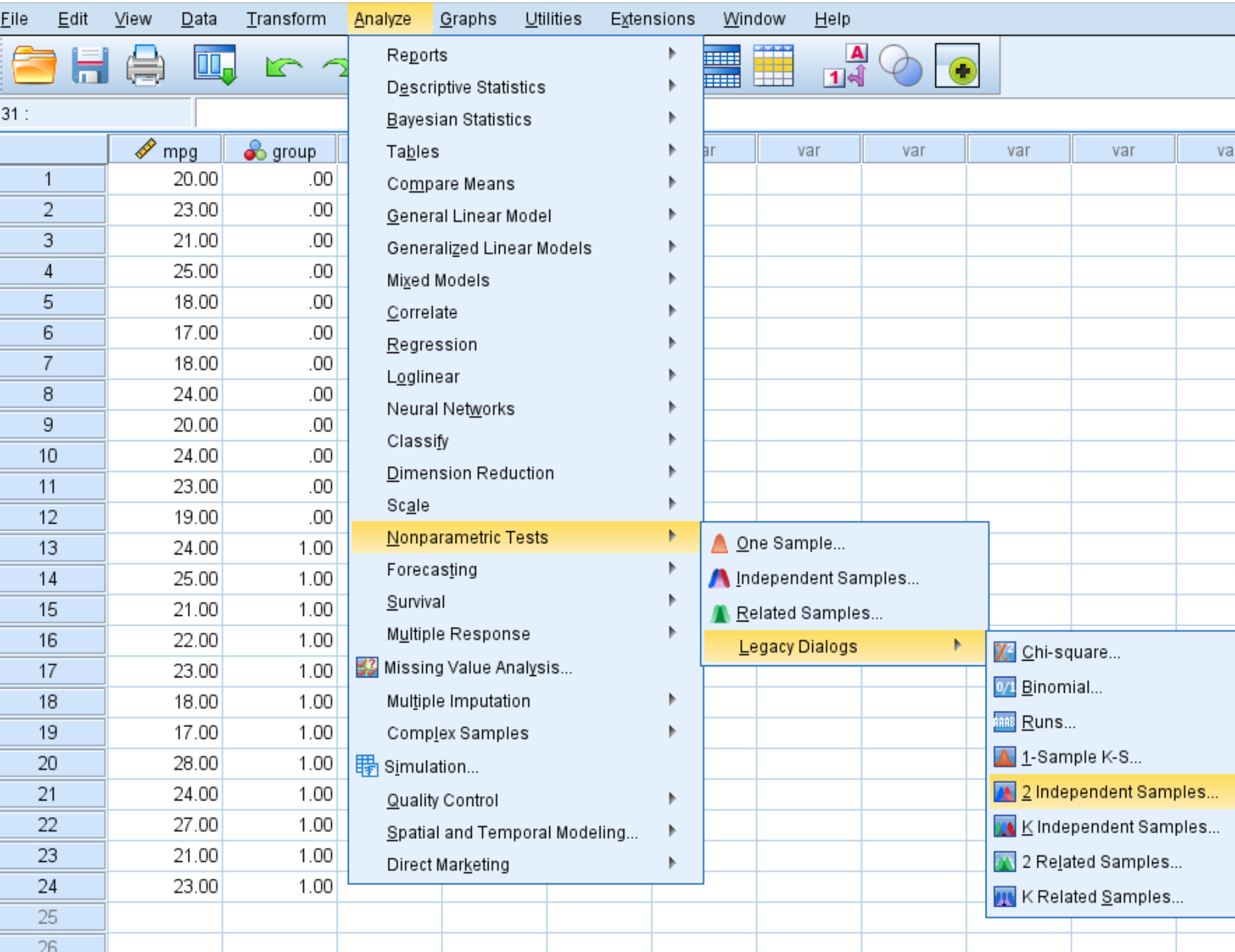
步骤2:填写必要的值以执行测试。
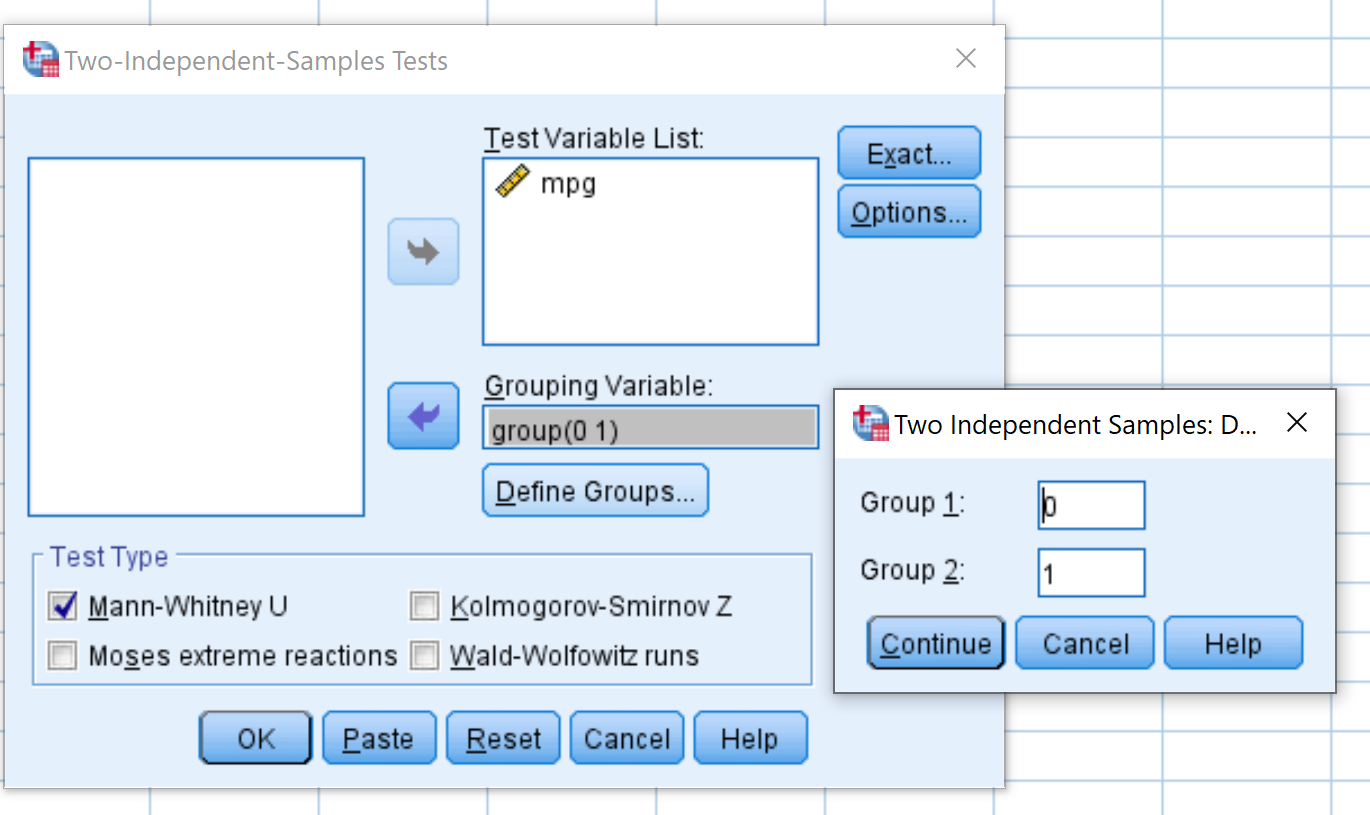
将mpg拖到标记为Test Variable List 的区域中,并将其分组到标记为Grouping Variable的区域中。单击定义组并将组 1 定义为值为 0 的行,将组 2 定义为值为 1 的行。
确保选中Mann-Whitney U旁边的框。然后单击“确定” 。
第 3 步:解释结果。
单击“确定”后,将显示 Mann-Whitney U 测试结果:
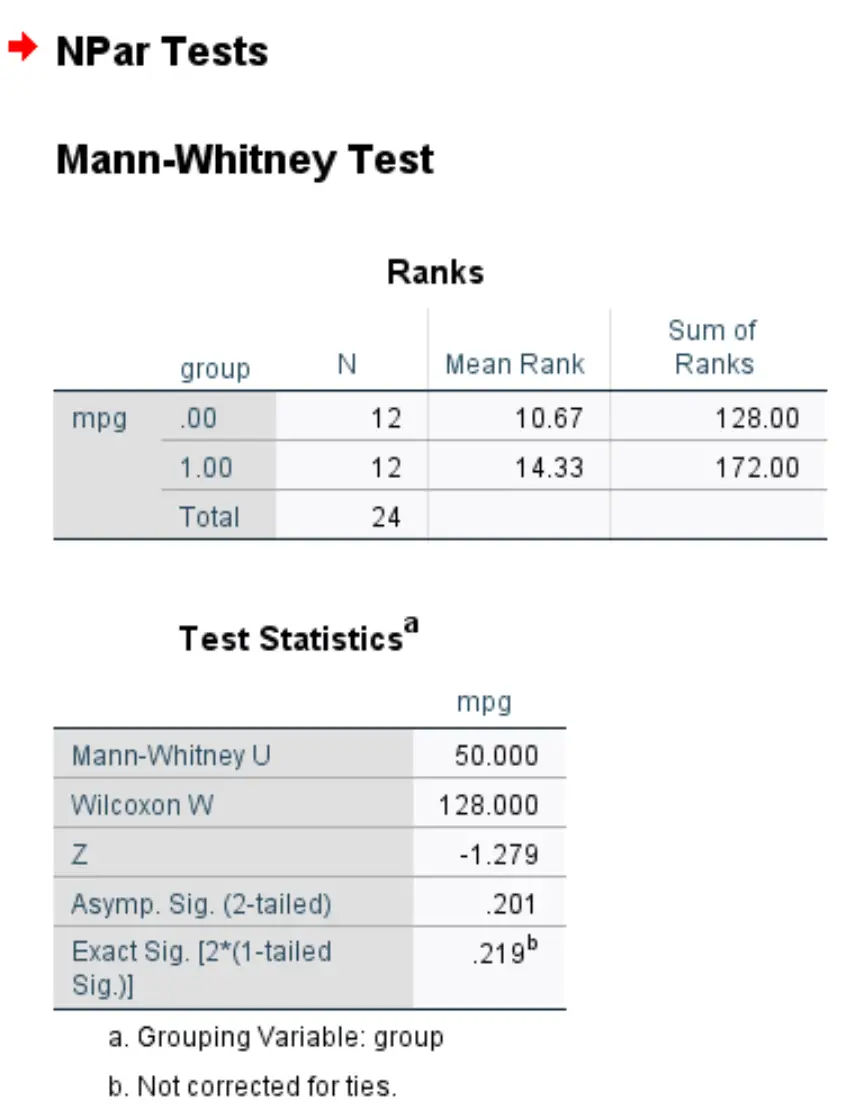
结果中最重要的数字是Z 检验统计量和两侧渐近p 值:
- Z 检验统计量: -1.279
- p 值: 0.201
由于 p 值不小于 0.05,因此我们无法拒绝原假设。我们没有足够的证据表明两组的真实平均英里数不同。
第四步:报告结果。
最后,我们将报告 Mann-Whitney U 测试的结果。以下是如何执行此操作的示例:
对 24 辆汽车进行了 Mann-Whitney U 测试,以确定新的燃油处理是否会导致每加仑平均里程数的差异。每组有12辆车。
结果显示,两组之间的平均 mpg 没有统计学差异(z = -1.279,p = 0.2010),显着性水平为 0.05。
根据这些结果,新的燃油处理不会对汽车每加仑行驶的里程产生重大影响。