如何在 stata 中执行 mann-whitney u 检验
当样本分布不呈正态分布且样本量较小 (n < 30) 时, Mann -Whitney U 检验(有时称为 Wilcoxon 秩和检验)用于比较两个样本之间的差异。它被认为是双样本 t 检验的非参数等效项。
本教程介绍如何在 Stata 中执行 Mann-Whitney U 检验。
示例:Stata 中的 Mann-Whitney U 检验
研究人员想知道燃油处理是否会导致汽车平均英里/加仑的变化。为了测试这一点,他们进行了一项实验,测量了 12 辆经过燃油处理的汽车和 12 辆未经燃油处理的汽车的每加仑英里数。
由于样本量很小,并且他们怀疑样本分布不是正态分布,因此他们决定进行 Mann-Whitney U 检验,以确定两组之间的 mpg 是否存在统计上的显着差异。
完成以下步骤以在 Stata 中执行 Mann-Whitney U 检验。
第 1 步:加载数据。
首先,通过在命令框中键入use https://www.stata-press.com/data/r13/fuel2并单击 Enter 来加载数据。
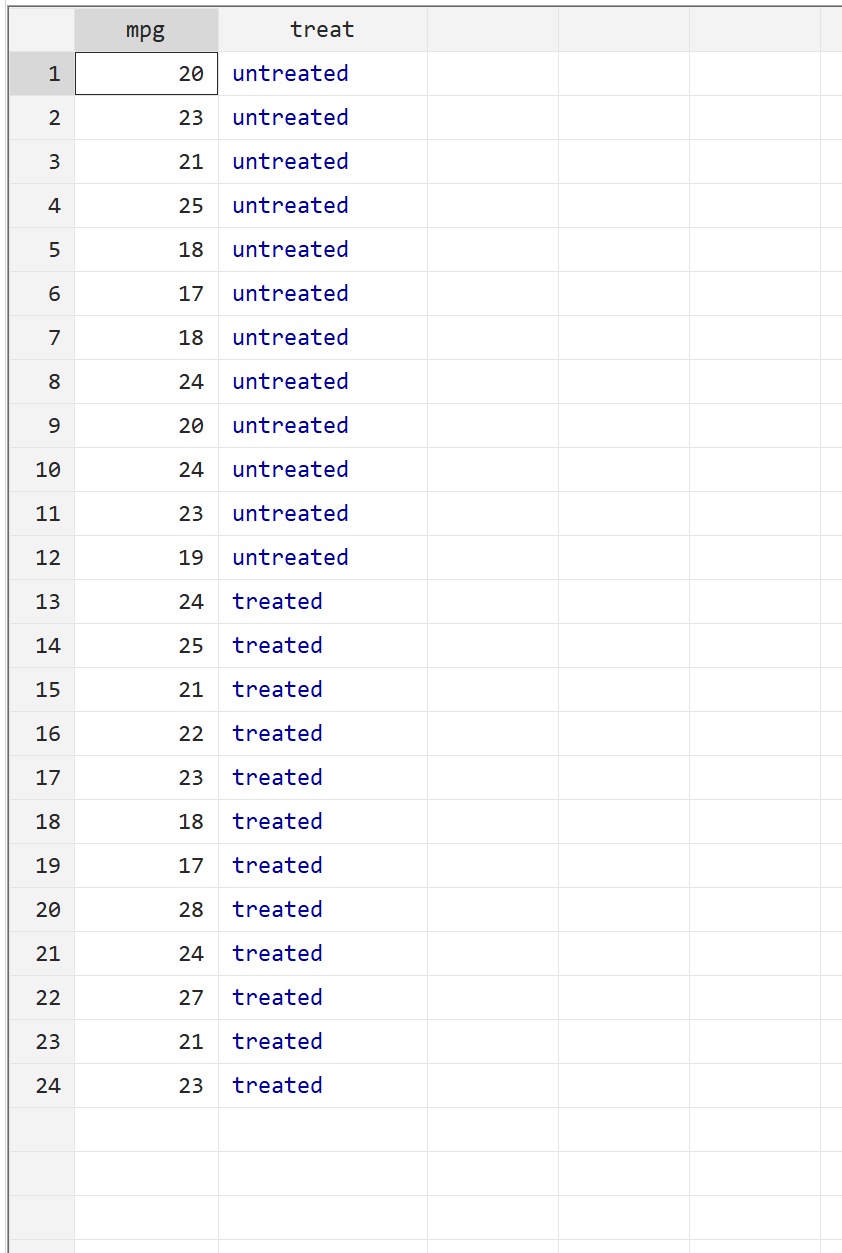
步骤2:查看原始数据。
在进行 Mann Whitney U 检验之前,我们首先看一下原始数据。从顶部菜单栏中,导航至数据 > 数据编辑器 > 数据编辑器(浏览) 。第一列mpg表示给定汽车的 mpg,而第二列Treat表示汽车是否接受了燃油处理。
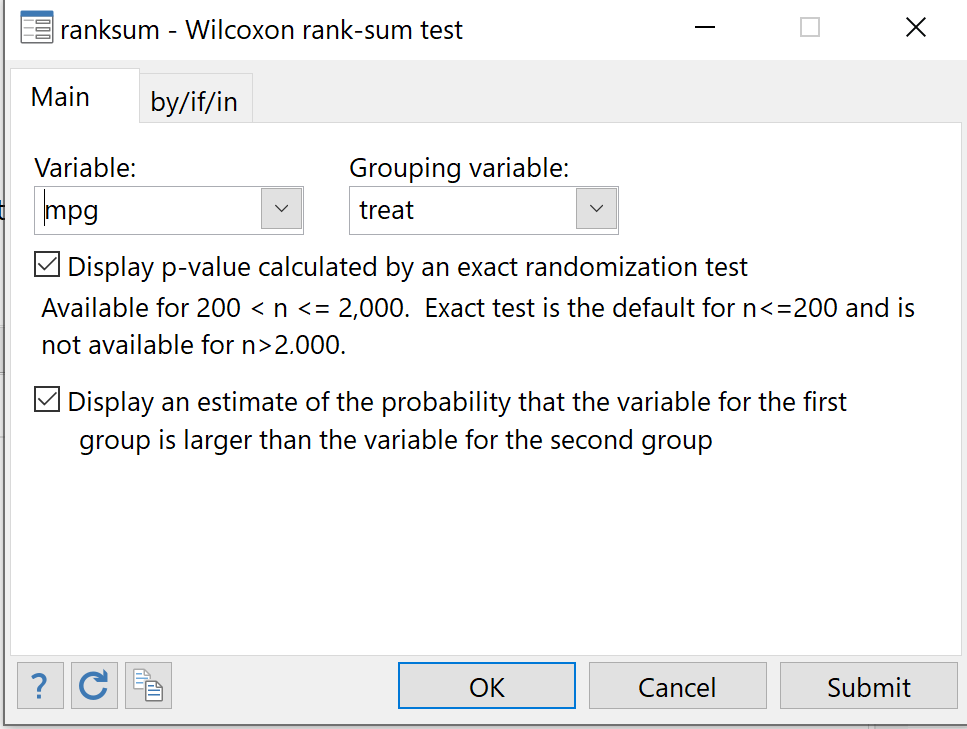
步骤 3:执行 Mann-Whitney U 检验。
从顶部菜单栏,导航到统计 > 摘要、表格和检验 > 非参数假设检验 > Wilcoxon 秩和检验。
对于变量,选择mpg 。对于分组变量,选择Treat 。选中下面的两个框以显示精确检验的 p 值,并显示第一组中的变量大于第二组中的变量的概率估计。最后,单击“确定” 。
测试结果将显示:
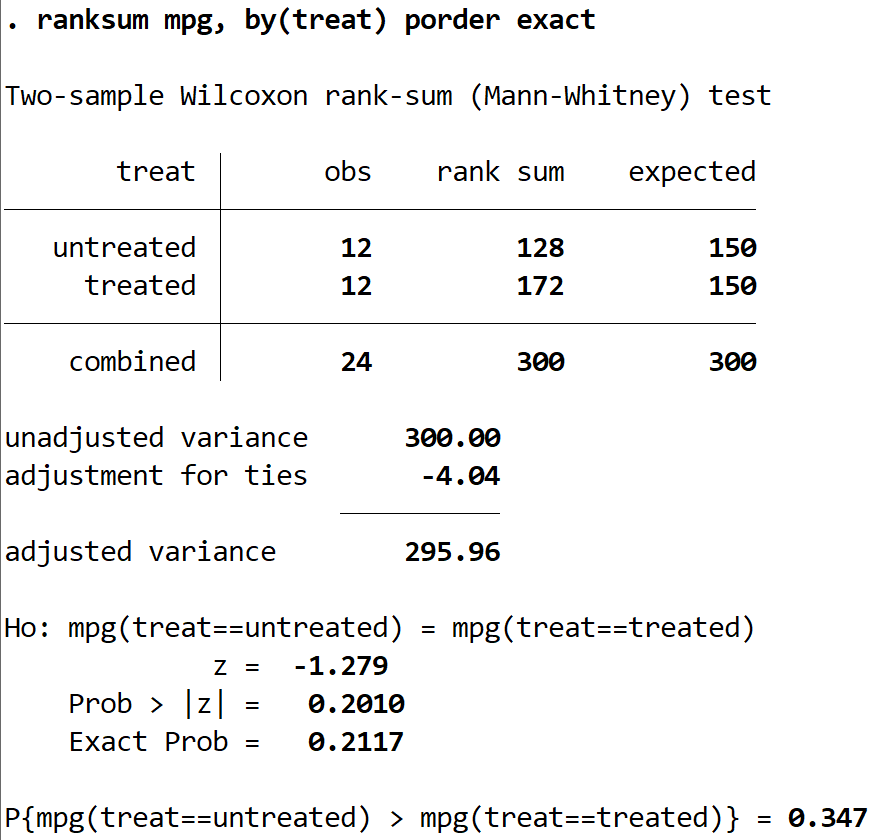
我们主要感兴趣的值是z = -1.279 和Prob > |z| = 0.2010。
由于检验的 p 值 (0.2010) 不小于我们的显着性水平 0.05,因此我们无法拒绝原假设。我们没有足够的证据表明两组的真实平均英里数不同。
第五步:报告结果。
最后,我们将报告 Mann-Whitney U 测试的结果。以下是如何执行此操作的示例:
对 24 辆汽车进行了 Mann-Whitney U 测试,以确定新的燃油处理是否会导致每加仑平均里程数的差异。每组有12辆车。
结果显示,两组之间的平均 mpg 没有统计学差异(z = -1.279,p = 0.2010),显着性水平为 0.05。
根据这些结果,新的燃油处理不会对汽车每加仑行驶的里程产生重大影响。