如何使用 python 执行 mann-kendall 趋势检验

Mann-Kendall 趋势检验用于确定时间序列数据是否存在趋势。这是非参数检验，意味着不对数据的正态性做出任何基本假设。

检验假设如下：

H ₀ （零假设）：数据中不存在趋势。

H _A （替代假设）：数据中存在趋势。 （这可能是积极的或消极的趋势）

如果检验的 p 值低于一定的显着性水平（常见选择为 0.10、0.05 和 0.01），则有统计显着性证据表明时间序列数据中存在趋势。

本教程介绍如何在 Python 中执行 Mann-Kendall 趋势检验。

示例：Python 中的 Mann-Kendall 趋势检验

要在 Python 中执行 Mann-Kendall 趋势测试，我们将首先安装pymannkendall包：

 pip install pymannkendall

一旦我们安装了这个包，我们就可以对时间序列数据集执行 Mann-Kendall 趋势测试：

 #create dataset
data = [31, 29, 28, 28, 27, 26, 26, 27, 27, 27, 28, 29, 30, 29, 30, 29, 28]

#perform Mann-Kendall Trend Test
import pymannkendall as mk

mk. original_test (data)

Mann_Kendall_Test(trend='no trend', h=False, p=0.422586268671707,
                  z=0.80194241623, Tau=0.147058823529, s=20.0,
                  var_s=561.33333333, slope=0.0384615384615, intercept=27.692307692)

以下是如何解释测试结果：

• 趋势：这表明趋势。可能的结果包括增加、减少或无趋势。
• h：如果存在趋势，则为 true。如果不存在趋势，则为 False。
• p：检验的 p 值。
• z：归一化检验统计量。
• 塔乌：肯德尔·塔乌。
• s： Mann-Kendal 分数
• var_s：偏差S
• 斜率： Theil-Sen/斜率估计器
• 拦截：拦截坚固的肯德尔-泰尔线

我们感兴趣的主要值是 p 值，它告诉我们数据中是否存在统计上显着的趋势。

在此示例中，p 值为0.4226 ，不小于 0.05。因此，时间序列数据不存在显着趋势。

除了执行 Mann-Kendall 趋势检验之外，我们还可以使用 Matplotlib 创建快速线图来可视化实际时间序列数据：

 import matplotlib. pyplot as plt

plt. plot (data)

次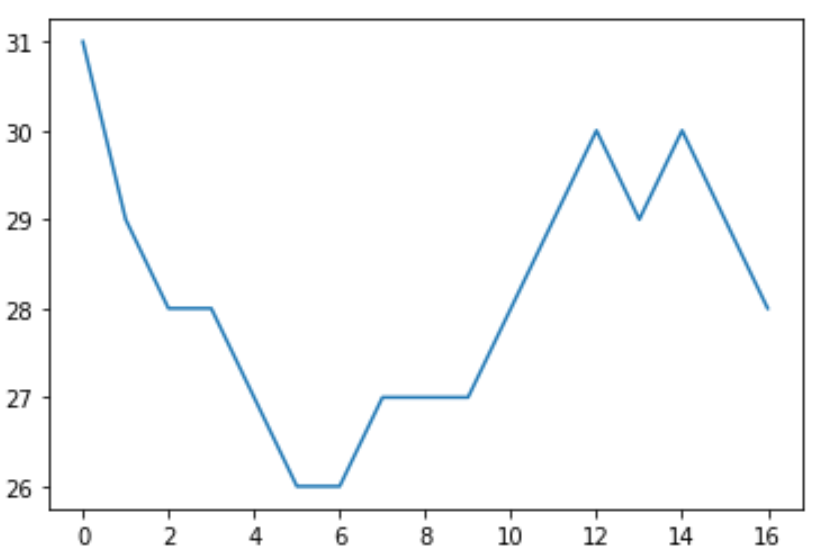

从图表中我们可以看到数据有点分散，这证实了数据没有明显的趋势。

其他资源

如何在 Matplotlib 中绘制时间序列
如何在 Python 中执行增强的 Dickey-Fuller 测试
如何从 Pandas DataFrame 绘制多个系列