有或没有重复的方差分析：有什么区别？
双向方差分析用于确定两个预测变量（或“因素”）是否对响应变量具有统计显着影响。
有两种不同类型的双向方差分析模型：
1. 不重复的双向方差分析
- 对于预测变量水平的每种组合，只有一个观测值。
2. 带有复制的双向方差分析
- 对于预测变量水平的每个组合，都有多个观察值。
例如，植物学家可能想知道阳光照射（无、低、中、高）和浇水频率（每天、每周）是否对植物生长有统计上的显着影响。
她可以执行以下双向方差分析模型之一：
1. 不重复的双向方差分析
使用这种方法，植物学家只需测量阳光水平和浇水频率的每种组合的植物生长情况。
例如，它测量了未暴露在阳光下且每天浇水的植物的生长情况。
接下来，她在没有暴露在阳光和每周浇水的情况下测量了单株植物的生长情况。
等等。
下表显示了没有复制的双向方差分析可能是什么样子：
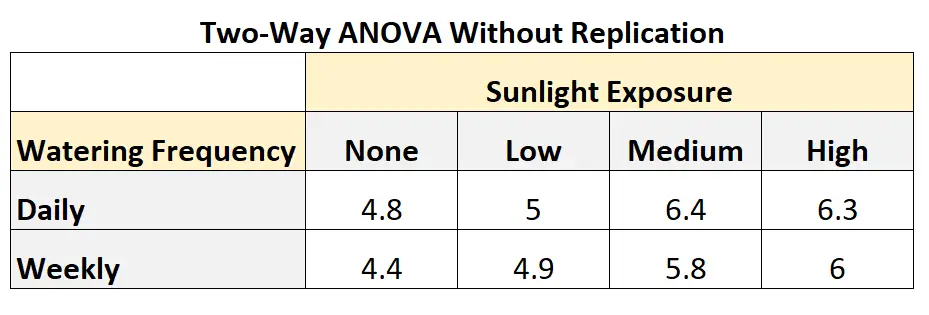
从表中我们可以看出：
- 没有暴露在阳光下且每天浇水的植物生长了4.8英寸。
- 没有阳光照射、没有每周浇水的植物生长了4.4英寸。
- 阳光照射较少且每天浇水的植物生长了5英寸。
- 阳光照射较少且每周浇水的植物生长了4.9英寸。
等等。
2. 带有复制的双向方差分析
使用这种方法，植物学家可以测量多种植物在阳光水平和浇水频率的每种组合下的生长情况。
例如，它可以测量五种不暴露在阳光下且每天不浇水的不同植物的生长情况。
接下来，她测量了其他五种植物在没有暴露在阳光下且没有每周浇水的情况下的生长情况。
等等。
下表显示了带有复制的双向方差分析可能是什么样子：
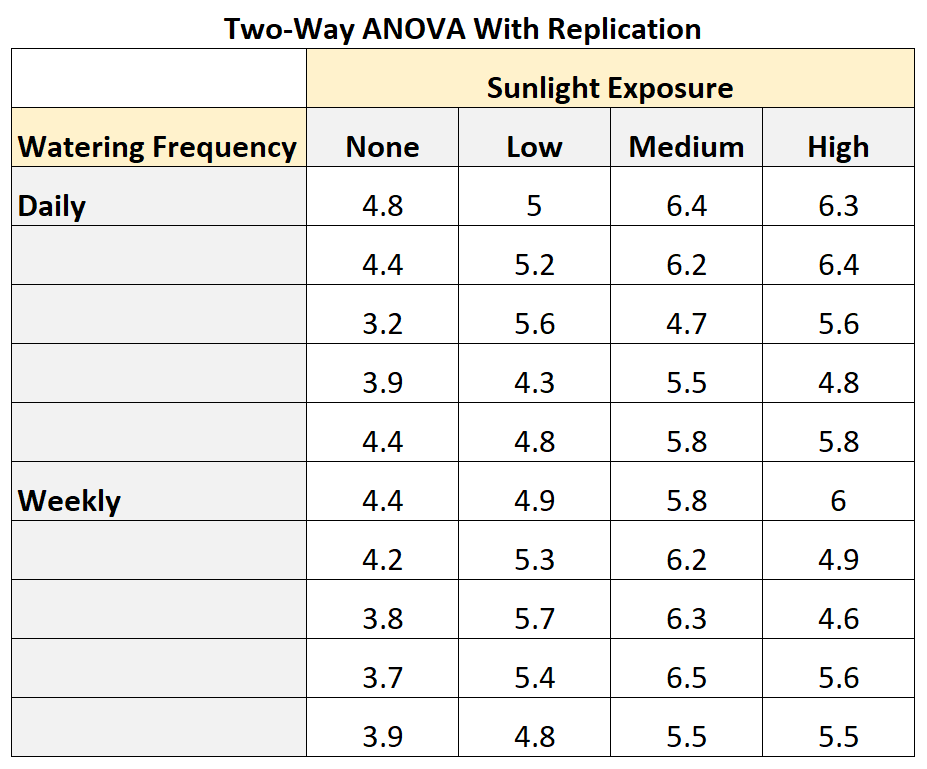
从表中我们可以看出：
- 没有阳光照射且每天浇水的植物可以生长4.8英寸。
- 另一种不暴露在阳光下且每天浇水的植物生长了4.4英寸。
- 另一种不暴露在阳光下且每天浇水的植物生长了3.2英寸。
等等。
有复制和无复制的方差分析之间的差异
具有复制的 ANOVA 模型与不具有复制的 ANOVA 模型之间的最大区别在于，具有复制的 ANOVA 只能测量两个预测变量之间的交互作用。
交互效应意味着两个预测变量之间存在某种类型的交互，这可能会影响我们解释预测变量和响应变量之间关系的方式。
例如，植物学家可能想知道阳光照射和浇水频率是否会影响植物生长。
尽管这两个预测变量有可能影响植物生长，但它们也有可能相互作用。
例如，暴露在阳光下可能会导致植物以不同的速度生长，具体取决于植物是每天还是每周浇水。
在这种情况下，阳光照射和浇水频率之间存在相互作用。
然而，衡量交互作用的唯一方法是对预测变量的每个水平组合进行多种测量。
Excel 中具有和不具有复制的方差分析
如果我们在 Excel 中执行双向方差分析而不进行复制，结果将如下所示：
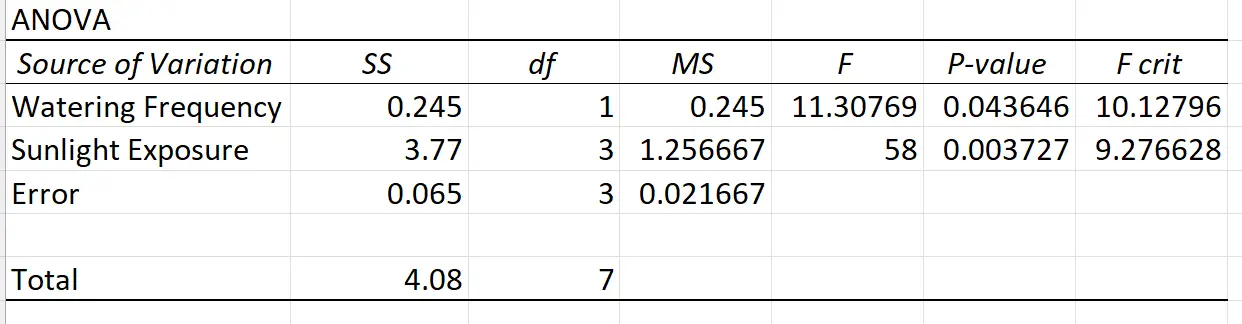
由于日照暴露和浇水频率的方差分析表中的 p 值小于 0.05，因此我们得出结论，这两个变量对植物生长具有统计上显着的影响。
但请注意，方差分析表中不包含交互项，因此我们不知道两个预测变量之间是否存在交互作用。
另一方面，如果我们在 Excel 中执行带有复制的双向方差分析，结果将如下所示：
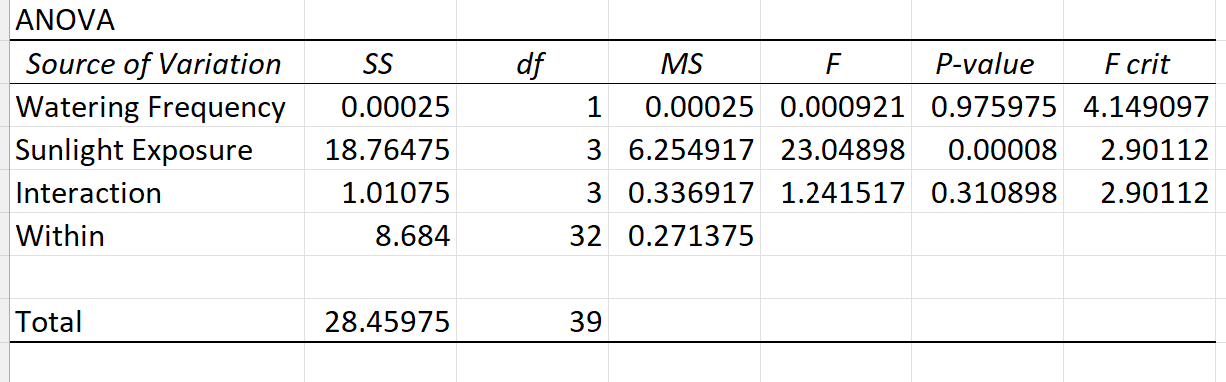
请注意，此方差分析表包含阳光照射、浇水频率以及这两个预测变量之间的交互作用的 p 值。
从表中我们可以看出，浇水频率不具有统计显着性，阳光照射具有统计显着性，并且两个预测变量之间不存在交互作用，不具有统计显着性。
这意味着我们可以得出关于阳光照射对植物生长的影响的结论，无论浇水频率如何。
其他资源
以下教程提供有关双向方差分析模型的其他信息：
关于作者
本杰明·安德森博
大家好，我是本杰明，一位退休的统计学教授，后来成为 Statorials 的热心教师。 凭借在统计领域的丰富经验和专业知识，我渴望分享我的知识，通过 Statorials 增强学生的能力。了解更多