Ti-84：如何找到概率分布的期望值

概率分布告诉我们随机变量取特定值的概率。

例如，以下概率分布告诉我们某支足球队在给定比赛中进球一定数量的概率：

为了找到概率分布的期望值，我们可以使用以下公式：

µ = Σx * P(x)

金子：

• x：数据值
• P(x)：价值概率

例如，足球队的预期进球数计算如下：

μ = 0*0.18 + 1*0.34 + 2*0.35 + 3*0.11 + 4*0.02 = 1.45 个进球。

以下分步示例展示了如何在 TI-84 计算器上计算概率分布的期望值。

第 1 步：输入数据

首先，我们将输入数据。

按统计，然后按编辑。然后在L1列中输入数据值，并在L2中输入它们的概率：

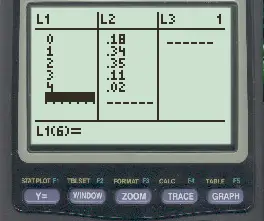
步骤 2：将两列相乘

接下来，我们将 L1 列和 L2 列相乘。

突出显示 L3 列的顶部并键入以下公式： L1 * L2

使用以下步骤输入此公式：

• 按统计，然后按1 。
• 按乘以x按钮。
• 按统计，然后按2 。

一旦按下Enter ，以下值将出现在 L3 列中：

第 3 步：找到期望值

最后，按照以下步骤求概率分布的期望值：

• 按2nd ，然后按MODE返回主屏幕。
• 按2nd ，然后按STAT 。滚动到“数学”，然后按5 。
• 按2，然后按3 。
• 按)按钮。

一旦按Enter ，将显示预期值：

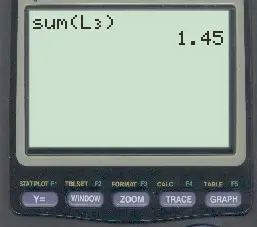
预期值为1.45 。

请注意，这与我们在文章开头手动计算的预期值相符。

其他资源

如何在 TI-84 计算器上查找样本的方差
如何在 TI-84 计算器上查找四分位数范围
如何在 TI-84 计算器上计算相对频率