现实生活中计算期望值的 5 个例子
期望值是一个告诉我们随机变量在无限次试验中的期望平均值的值。
我们使用以下公式来计算事件的期望值:
期望值= Σx * P(x)
金子:
- x :数据值
- P(x) :价值概率
这个公式可能看起来有点令人困惑,但是当您看到它在现实世界的示例中使用时,它会更有意义。
以下示例显示了如何在五种不同的现实情况下计算预期值。
示例 1:投资
贸易公司经常使用预期值来确定投资的预期利润或损失。
例如,假设一项特定投资可以以 0.95 的概率产生 5% 的年回报率,但也可以以 0.05 的概率产生 -20% 的年回报率。
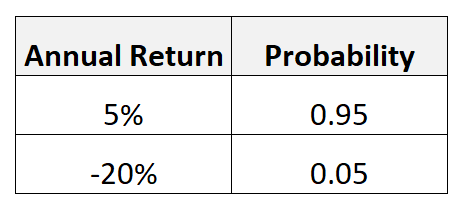
我们将计算这项投资的预期价值如下:
- 预期值 = 5%*.95 + (-20%)*.05 = 3.75%
这项特殊的投资具有积极的预期价值。
这意味着,如果我们对这项特定投资进行无限次投资,我们预计长期平均年回报率为 3.75%。
示例 2:天气
农业公司经常使用预期值来确定给定季节的预期降雨量。
例如,假设有 20% 的可能性发生 1 英寸的降雨,70% 的可能性发生 2 英寸的降雨,10% 的可能性发生 3 英寸的降雨。
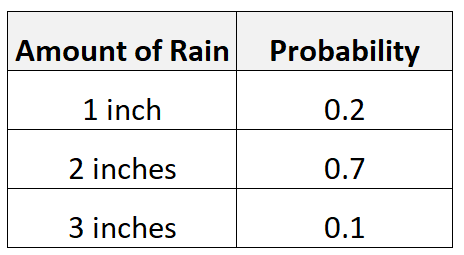
我们将计算降雨量的预期值如下:
- 预期值 = 0.2*1 + 0.7*2 + 0.1*3 = 1.9 英寸
示例 3:机会游戏
玩家经常使用期望值来确定他们在给定游戏中可能赢得的金额。
例如,假设在某个游戏中,有 5% 的机会赢得 100 美元,有 50% 的机会赢得 0 美元,有 45% 的机会失去 20 美元。
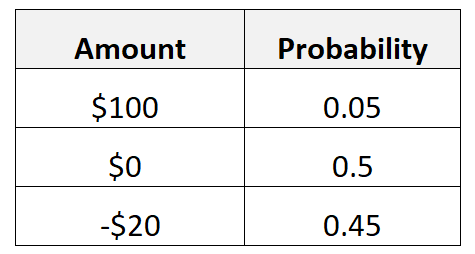
我们将计算收益的预期值如下:
- 预期值 = 0.05*100$ + 0.5*0$ + 0.45*(-20$) = -4$
这意味着,如果我们无限次地玩这个游戏,我们预计每次玩时平均会损失 4 美元。
示例 4:商业
企业经常使用期望值来计算广告支出的预期回报。
例如,假设对于特定广告,有 10% 的机会收到 5 美元的回报,30% 的机会收到 2 美元的回报,60% 的机会收到 – 8 美元的回报。
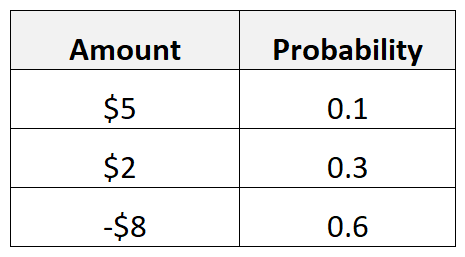
我们将计算广告的预期价值如下:
- 预期值 = 0.1*5$ + 0.3*2$ + 0.6*(-8$) = -3.70$
这个特定的广告具有负的期望值。
这意味着,如果该公司无限次使用该特定广告,则预计每次平均损失 3.70 美元。
例子5:创业
期望值经常被个人用来决定是否追求创业。
例如,假设一个人认为,如果他辞去工作并成为自营职业者,他有 60% 的机会在第一年赚到 20,000 美元,30% 的机会赚到 60,000 美元,10% 的机会赢得 20,000 美元。 0 美元。
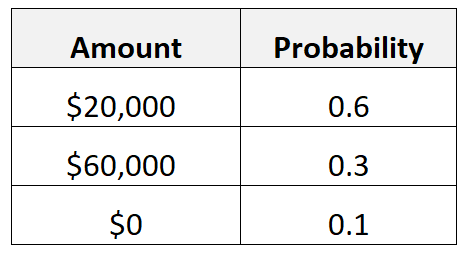
我们将他们创业第一年的收入预期值计算如下:
- 预期价值 = 0.6*$20,000 + 0.3*$60,000 + 0.1*$0 = $30,000
根据这笔钱是否足够,个人可以选择保留或离开目前的工作。
其他资源
以下教程提供有关预期值的其他信息: