Durbin-watson 测试:定义和示例
线性回归的主要假设之一是连续残差之间不存在相关性。换句话说,我们假设残差是独立的。
当违反此假设时,回归模型中系数的标准误差可能会被低估,这意味着预测变量在统计上不显着时更有可能被认为具有统计显着性。现实中并不存在。
确定是否满足此假设的一种方法是执行Durbin-Watson检验,该检验用于检测回归残差中是否存在自相关。
执行 Durbin-Watson 测试的步骤
Durbin-Watson 检验使用以下假设:
H 0 (零假设):残差之间不存在相关性。
H A (替代假设):残差是自相关的。
Durbin-Watson 检验的检验统计量(通常表示为d )计算如下:
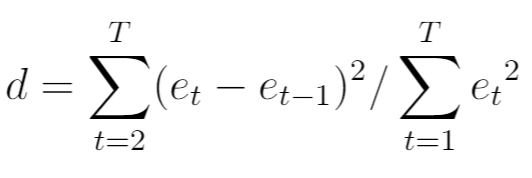
金子:
- T:观察总数
- et t :回归模型的第t个残差
检验统计量的范围始终为 0 到 4,其中:
- d = 2 表示无自相关
- d < 2 表示正序列相关
- d > 2 表示负序列相关
一般来说,如果d小于1.5或大于2.5,则可能存在严重的自相关问题。否则,如果d介于 1.5 和 2.5 之间,则自相关可能不是问题。
要确定 Durbin-Watson 检验统计量在某个 alpha 水平下是否显着显着,您可以参考此临界值表。
如果 Durbin-Watson 检验统计量的绝对值大于表中的值,则您可以拒绝检验的原假设并得出自相关存在的结论。
如果检测到自相关该怎么办
如果您拒绝 Durbin-Watson 检验的零假设并得出残差中存在自相关的结论,那么如果您认为问题足够严重,则可以采用多种不同的选项来纠正该问题:
- 对于正序列相关,请考虑向模型添加因变量和/或自变量的滞后。
- 对于负序列相关,请确保没有任何变量过度延迟。
- 对于季节性相关性,请考虑向模型添加季节性虚拟变量。
这些策略通常足以消除自相关问题。
执行 Durbin-Watson 检验的示例
有关 Durbin-Watson 检验的分步示例,请参阅以下教程,其中解释了如何使用不同的统计软件执行检验:
如何在 R 中执行 Durbin-Watson 测试
如何在 Python 中执行 Durbin-Watson 测试
如何在 Excel 中执行 Durbin-Watson 检验