条件概率（或条件概率）

在这里您将了解什么是条件概率（或条件概率）。我们通过示例解释如何计算条件概率以及此类概率的属性。此外，您将能够通过逐步解决的条件概率练习进行练习。

什么是条件概率？

条件概率，也称为条件概率，是一种统计度量，表示如果另一个事件 B 发生，则事件 A 发生的概率。即，条件概率P(A|B)是指事件B已经发生之后事件A发生的概率。

条件概率在两个事件之间用竖线书写：P(A|B)，内容为：“给定事件 B 时事件 A 的条件概率”。

请注意，条件概率值是 0 到 1 之间的数字。条件概率越高，事件 B 发生时事件 A 发生的可能性越大，但条件概率越低，事件 A 发生的可能性越小当事件 B 发生时，也会发生。

条件概率公式

事件 A 给定事件 B 的条件概率等于事件 A 和事件 B 相交的概率除以事件 B 的概率。

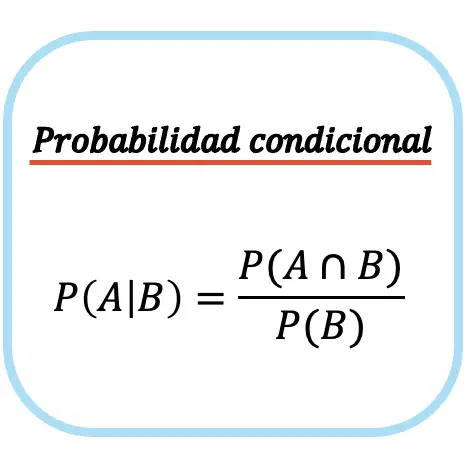
注意，只有当无条件事件发生的概率非零，即P(B)≠0时，才可以使用条件概率（或条件概率）公式。或者换句话说，事件B是否有可能发生。

条件概率也可以从其倒数计算出来，即如果P(B|A)已知，则可以确定P(A|B)。但要做到这一点，你必须应用贝叶斯定理，你可以在这里看到这个定理的内容：

条件概率的例子

一旦我们了解了条件概率的定义和公式是什么，我们将逐步解决此类概率的示例，以充分理解其含义。

• 在对一个 30 名学生的班级进行考试后，我们收集了数据以了解有多少学生学习了以及有多少人通过了考试。结果列于以下列联表中。根据收集的数据，计算通过考试的条件概率（如果您已经学习过）。

为了获得条件概率，我们必须应用之前看到的公式：

因此，我们首先需要求出一个学生学习再学习并通过的概率。要找到学生学习的概率，我们只需使用拉普拉斯规则，即将学习的学生人数除以观察总数：

我们可以通过学习并通过的学生人数除以总数，从列联表中找出学生同时学习和通过的概率：

因此，如果学生已经学习，他通过考试的概率为：

相关事件和独立事件的条件概率

在本节中，我们将了解条件概率与相关事件和独立事件（或相关事件和独立事件）之间的关系。因为，虽然它们是不同的概念，但这两种类型的事件都与条件概率相关。

当两个事件（或事件）发生的概率不相互依赖时，它们就是独立的。在这种情况下，两个事件之间的交集相当于每个事件各自的概率的乘积。因此，条件概率公式被简化：

简而言之，如果事件 A 和 B 是独立的，则事件 A 给定事件 B 的条件概率恰好等于事件 A 发生的概率。

另一方面，当两个事件相关时，意味着一个事件的概率取决于另一个事件的概率。因此，当两个事件 A 和 B 相关时，事件 A 给定事件 B 的条件概率与事件 A 发生的概率不同。

解决了条件概率练习

练习1

我们知道，在装满球的袋子里，一半是橙色的，另一半是绿色的。此外，三分之一的球是橙色的，同时标有标志。当你画一个橙色的球时，它收到信号的概率是多少？

为了解决这个练习，我们必须应用条件概率公式，即：

问题陈述告诉我们，袋子的一半是橙子。因此，理论上捡到橙色球的概率是50%。

另一方面，我们知道总数的三分之一是橙色球并且有信号，因此获得带有信号的橙色球的概率为：

最后，我们将计算出的概率代入条件概率公式求得其值：

总之，如果信号是橙色，则抽到球的概率为 66%。

练习2

如果我们在一个盒子里有六支蓝笔和三支黑笔，计算画出一支蓝笔的概率和连续画出两支蓝笔的概率。

要确定拿起蓝笔一次的概率，只需使用拉普拉斯定律：

该问题还要求我们知道连续拿起两支蓝笔的概率，即如果我们之前已经拿起了一支蓝笔，则拿起一支蓝笔的条件概率。

如果我们画一支蓝色笔，我们的情况就不太有利，但总数也少了一支。因此，条件概率为：

练习3

如果抛硬币出现正面，则骰子掷到数字 4 的条件概率是多少？

要解决此练习，您必须考虑条件概率理论，因为“掷骰子得到数字 4”和“抛硬币得到正面”事件是独立的。因此不必使用条件概率公式，但满足以下等式：

因此，要找到条件概率，只需使用拉普拉斯规则即可：

练习4

研究了一个国家 25 家公司的财政年度以及它们的股价如何根据当年的经济结果变化。您可以在以下列联表中看到收集的数据：

如果一家公司在过去一年盈利，其股价上涨的可能性有多大？

该练习询问我们在公司取得积极的经济成果的情况下股票上涨的条件概率。因此，要计算这个概率，我们必须使用条件概率公式：

因此，我们首先计算一家公司盈利的概率，其次计算一家公司在提高每股价格的同时获得经济利润的概率：

然后我们将找到的值代入公式并计算条件概率：

条件概率的性质

条件概率或条件概率的性质如下：

• 给定事件 B 的事件 A 的条件概率加上给定事件 B 的互补事件 A 的条件概率之和等于 1。

• 如果事件 A 是事件 B 的子集，则当 B 为真时，A 将始终发生。因此，在这些情况下，事件 A 给定事件 B 的条件概率为 1。

• 给定两个不同的事件，以下关于条件概率的等式始终成立：