如何在 excel 中计算条件概率

假设事件B已发生，则事件A发生的条件概率计算如下：

P(A|B) = P(A∩B) / P(B)

金子：

P(A∩B)=事件A和事件B同时发生的概率。

P(B) = 事件 B 发生的概率。

在计算双向表的概率时，此公式特别有用，双向表是显示两个分类变量的频率（或“计数”）的表。

例如，下面的双向表显示了一项调查结果，该调查询问了 300 人他们喜欢哪种运动：棒球、篮球、橄榄球或英式足球。行显示受访者的性别，列表示他们选择的运动：

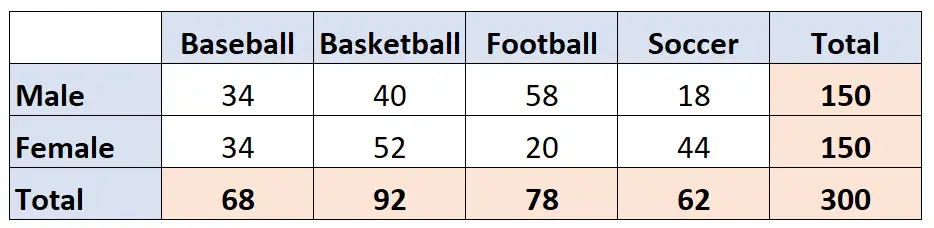
这是一个双向表，因为我们有两个分类变量：性别和最喜欢的运动。

然后我们将展示如何在 Excel 中计算双向表的条件概率。

如何在 Excel 中计算条件概率

假设我们想回答以下问题：

“考虑到受访者最喜欢的运动是棒球，他是男性的可能性有多大？” »

我们可以使用条件概率公式找到答案：

P(男|棒球) = P(男∩棒球) / P(棒球) = (34/300) / (68/300) = 0.5

因此，鉴于受访者最喜欢的运动是棒球，他是男性的概率为 0.5（或 50%）。

我们可以使用类似的公式计算表中其他场景的条件概率。下图显示了如何计算表中的每个条件概率以及所使用的公式：

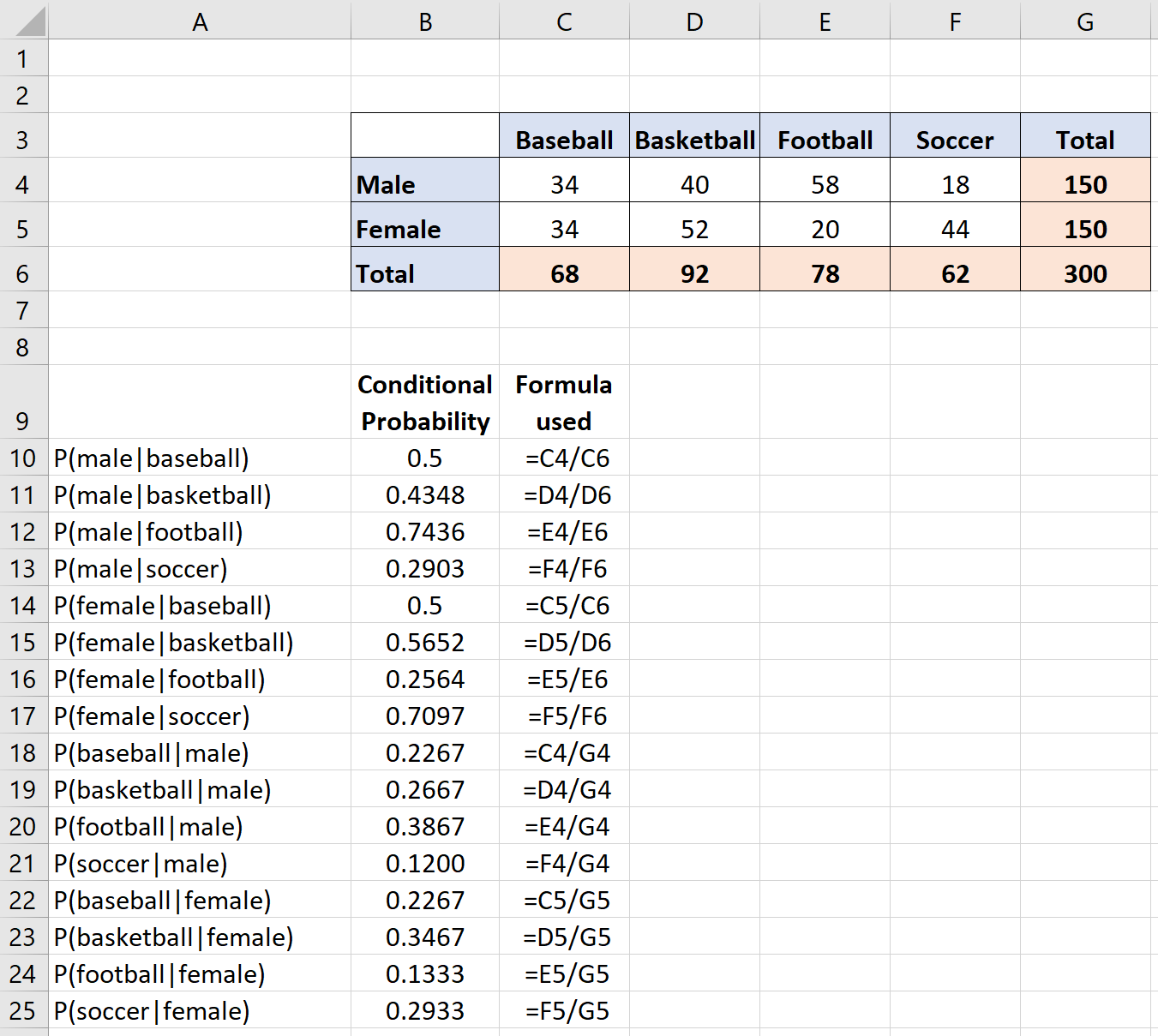
请注意，对于每个条件概率计算，我们仅使用条件概率公式 P(A|B) = P(A∩B) / P(B)。

例如，假设受访者是女性，她最喜欢的运动是足球的概率计算如下：

P(足球|女性) = P(足球∩女性) / P(女性)

在 300 名受访者中，恰好有 44 名女性，并且最喜欢足球作为她们最喜欢的运动，因此 P(足球∩女性) = 44/300。

在 300 名受访者中，有 150 名女性，因此 P（女性）= 150/300。

因此，P(足球|女性) = P(足球∩女性) / P(女性) = (44/300) / (150/300) = 0.2933 。

我们对每个条件概率场景执行类似的计算。

其他资源

如何在复式表中查找条件相对频率
什么是统计学中的条件分布？