标准化或规范化：有什么区别？

标准化和规范化是调整数据大小的两种方法。

归一化将数据集缩放为均值 0 和标准差 1。为此，它使用以下公式：

x_新= ( _xi – x ) / s

金子：

• x _i ：数据集的^{第 i 个}值
• x ：样本平均值
• s ：样本的标准差

归一化会调整数据集的大小，使每个值都介于 0 和 1 之间。它通过使用以下公式来实现此目的：

x_新= ( _xi – x_最小值) / (x_最大值– x_最小值)

金子：

• x _i ：数据集的^{第 i 个}值
• x _min ：数据集中的最小值
• x _max ：数据集中的最大值

以下示例展示了如何在实践中标准化和规范化数据集。

示例：如何标准化数据

假设我们有以下数据集：

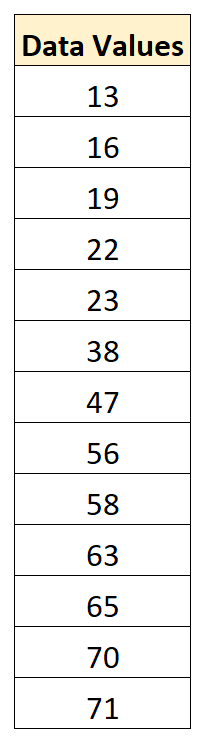
数据集中的平均值为 43.15，标准差为 22.13。

为了标准化13的第一个值，我们将应用之前共享的公式：

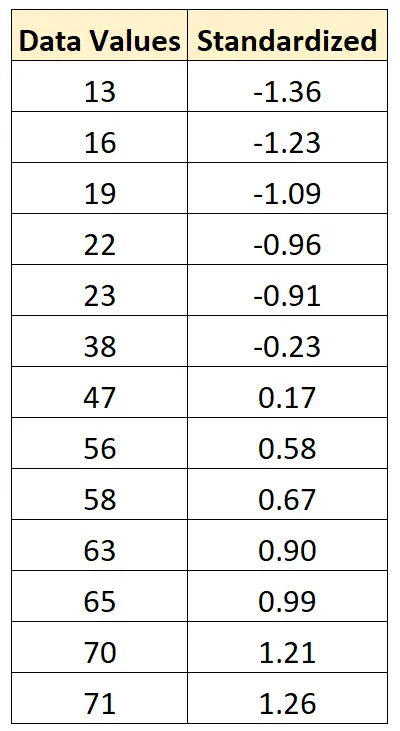
• x_新= ( _xi – x ) / s = (13 – 43.15) / 22.13 = -1.36

为了标准化16的第二个值，我们将使用相同的公式：

• x_新= ( _xi – x ) / s = (16 – 43.15) / 22.13 = -1.23

为了标准化第三个值19 ，我们将使用相同的公式：

• x_新= ( _xi – x ) / s = (19 – 43.15) / 22.13 = -1.09

我们可以使用这个完全相同的公式来标准化原始数据集中的每个值：

示例：如何标准化数据

再次假设我们有以下数据集：

数据集中的最小值为 13，最大值为 71。

为了标准化13的第一个值，我们将应用之前共享的公式：

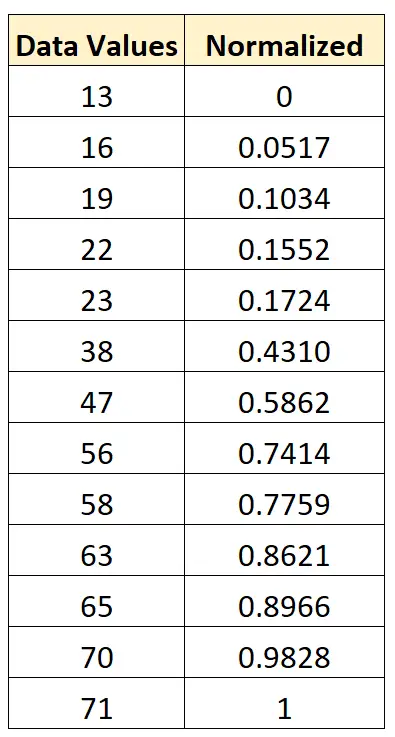
• x_新= ( _xi – x_最小值) / (x_最大值– x_最小值) = (13 – 13) / (71 – 13) = 0

为了标准化16的第二个值，我们将使用相同的公式：

• x_新= ( _xi – x_最小值) / (x_最大值– x_最小值) = (16 – 13) / (71 – 13) = 0.0517

为了标准化第三个值19 ，我们将使用相同的公式：

• x_新= ( _xi – x_最小值) / (x_最大值– x_最小值) = (19 – 13) / (71 – 13) = 0.1034

我们可以使用这个完全相同的公式将原始数据集中的每个值标准化为 0 到 1 之间：

标准化或规范化：何时使用它们？

通常，当我们进行某种类型的分析时，我们会标准化数据，其中我们有多个在不同尺度上测量的变量，并且我们希望每个变量具有相同的范围。

这可以防止一个变量产生不适当的影响，特别是当它以不同的单位测量时（即，如果一个变量以英寸为单位，另一个以码为单位）。

另一方面，当我们想知道数据集中的每个值与平均值的标准差有多少时，我们通常会对数据进行标准化。

例如，我们可能有一个特定学校 500 名学生的考试成绩列表，我们想知道每个考试成绩与平均成绩的标准差是多少。

在这种情况下，我们可以对原始数据进行标准化来了解这些信息。那么，标准化分数 1.26 将告诉我们该特定学生的考试分数比平均考试分数高出 1.26 个标准差。

无论您决定标准化还是规范化数据，请记住以下几点：

• 标准化数据集的值始终在 0 到 1 之间。
• 标准化数据集的平均值为 0，标准差为 1，但最大值和最小值没有特定的上限或下限。

根据您的特定场景，规范化或标准化数据可能更有意义。

其他资源

以下教程解释了如何在不同的统计软件中对数据进行标准化和归一化：

如何在 R 中标准化数据
如何在 Excel 中标准化数据
如何在 Python 中标准化数据
如何在 R 中标准化数据