什么是标准化检验统计量？

统计假设是关于总体参数的假设。例如，我们可以假设美国男性的平均身高是 70 英寸。关于身高的假设是统计假设，而美国男性的真实平均身高是人口参数。

假设检验是一种正式的统计检验，我们用它来拒绝或未能拒绝统计假设。

进行假设检验的基本过程如下：

1.收集样本数据。

2.计算样本数据的标准化检验统计量。

3.将标准化检验统计量与临界值进行比较。如果比临界值更极端，则拒绝原假设。否则，不要拒绝原假设检验。

我们用来计算标准化检验统计量的公式根据我们正在执行的假设检验的类型而有所不同。

下表显示了用于计算四种主要假设检验类型的标准化检验统计量的公式：

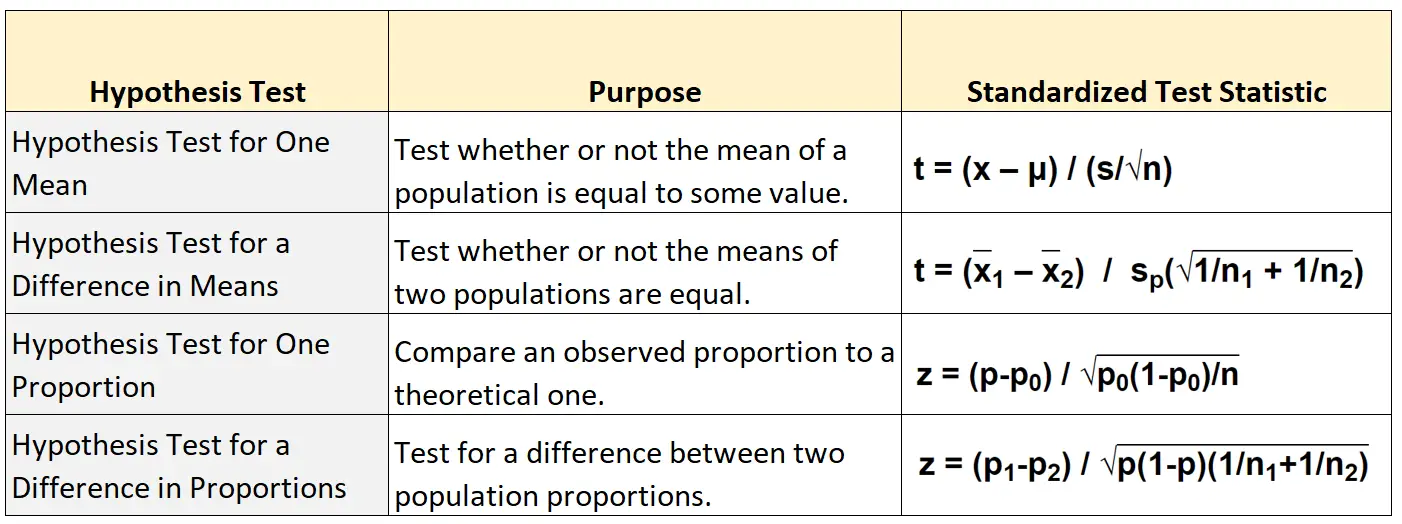
平均值的假设检验

单样本 t 检验用于测试总体平均值是否等于某个值。

此类测试的标准化测试统计量计算如下：

t = ( X – μ) / (s/√n)

金子：

• x：样本均值
• μ ₀ ：假设总体平均值
• s：样本标准差
• n：样本量

有关计算此标准化测试统计量的示例，请参阅本教程。

均值差异的假设检验

双样本 t 检验用于检验两个总体的均值是否相等。

此类测试的标准化测试统计量计算如下：

t = ( X ₁ – X ₂ ) / s _p (√ 1/n ₁ + 1/n ₂ )

其中 x ₁和 x ₂是样本均值，n ₁和 n ₂是样本大小，其中 s _p计算如下：

s _p = √ (n ₁ -1)s ₁ ² + (n ₂ -1)s ₂ ² / (n ₁ +n ₂ -2)

其中 s ₁ ²和 s ₂ ²是样本方差。

有关计算此标准化测试统计量的示例，请参阅本教程。

比例假设检验

单比例 z 检验用于将观察到的比例与理论比例进行比较。

此类测试的标准化测试统计量计算如下：

z = (pp ₀ ) / √ p ₀ (1-p ₀ )/n

金子：

• p：观察到的样本比例
• p ₀ ：假设的人口比例
• n：样本量

有关计算此标准化测试统计量的示例，请参阅本教程。

比例差异的假设检验

二比例 z 检验用于检验两个总体比例之间的差异。

此类测试的标准化测试统计量计算如下：

z = (p ₁ -p ₂ ) / √ p(1-p)(1/n ₁ +1/n ₂ )

其中 p ₁和 p ₂是样本比例，n ₁和 n ₂是样本大小，其中 p 是总合并比例，计算如下：

p = (p ₁ n ₁ + p ₂ n ₂ )/(n ₁ + n ₂ )

有关计算此标准化测试统计量的示例，请参阅本教程。