标准差和标准误差：有什么区别？

学生在统计学中经常混淆的两个术语是标准差和标准误差。

标准差衡量数据集中数值的分布情况。

标准误差是总体中重复样本平均值的标准偏差。

让我们看一个例子来清楚地说明这个想法。

示例：标准差与标准误差

假设我们测量 10 只不同海龟的重量。

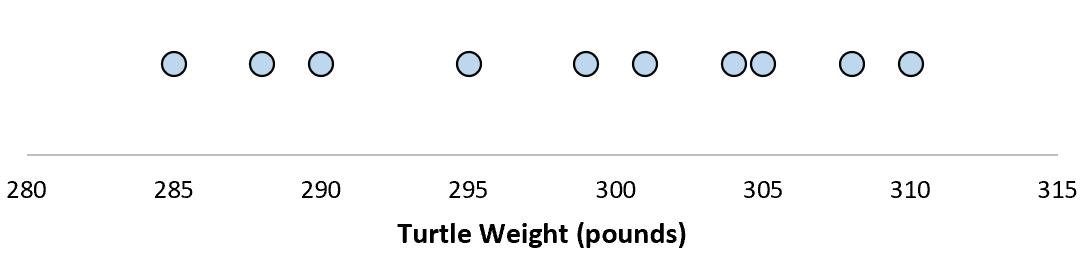
对于这个包含 10 只海龟的样本，我们可以计算样本均值和样本标准差：

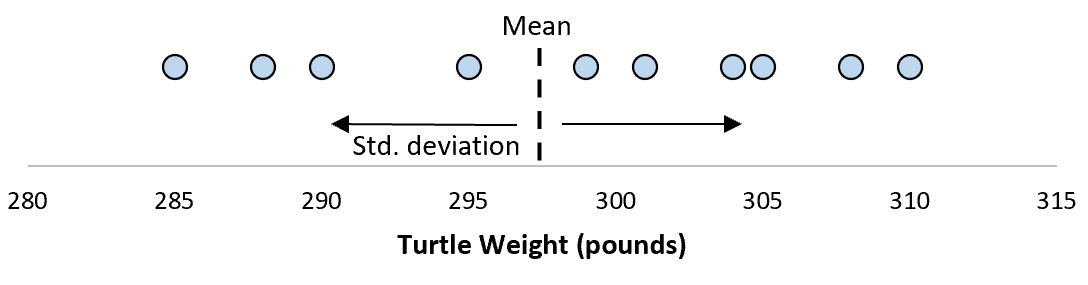
假设标准差为 8.68。这让我们了解了这些海龟的体重分布。

但假设我们又收集了 10 只海龟的简单随机样本，并对它们进行了测量。

尽管 10 只海龟来自同一种群，但它们的平均值和标准差很可能略有不同：

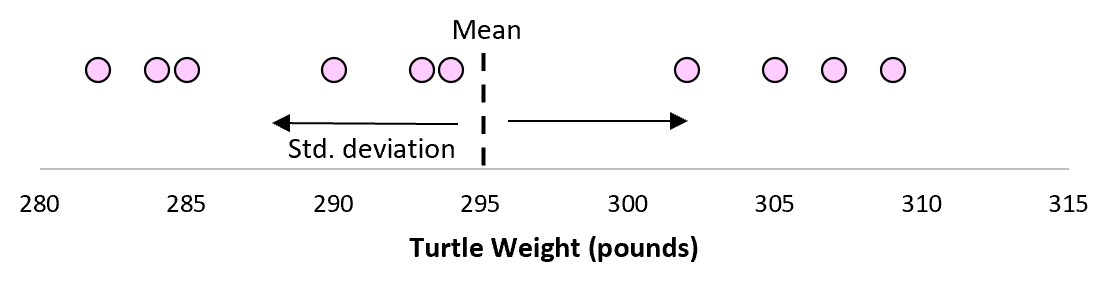
现在，如果我们想象我们从同一总体中提取重复样本并记录每个样本的样本均值和样本标准差：

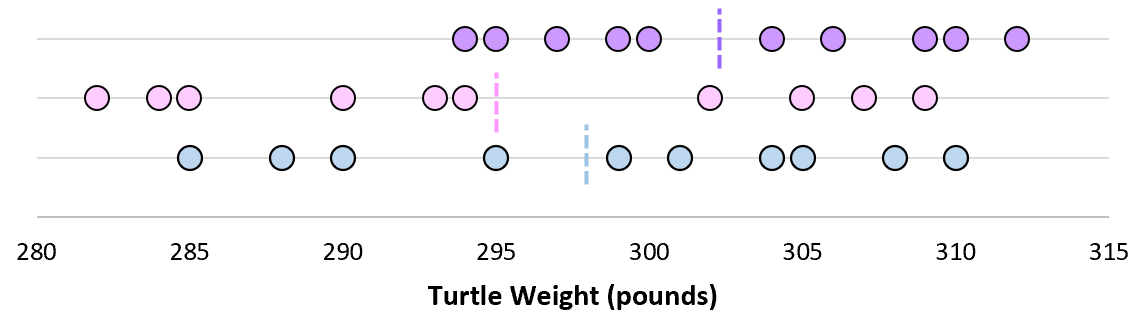
现在想象我们将每个样本均值绘制在同一条线上：

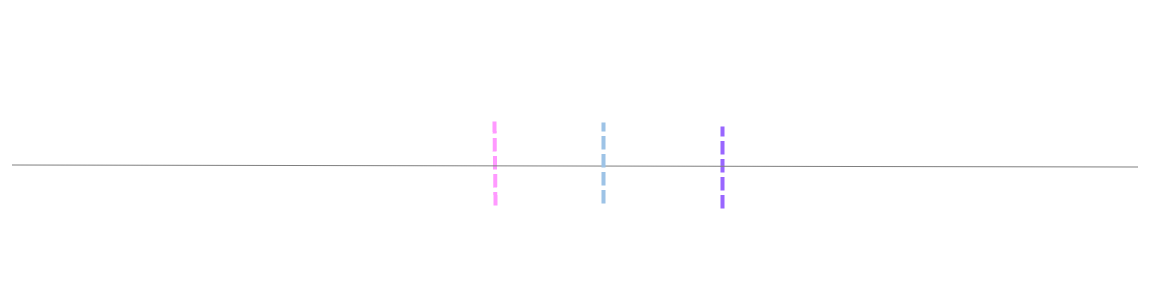
这些平均值的标准差称为标准误差。

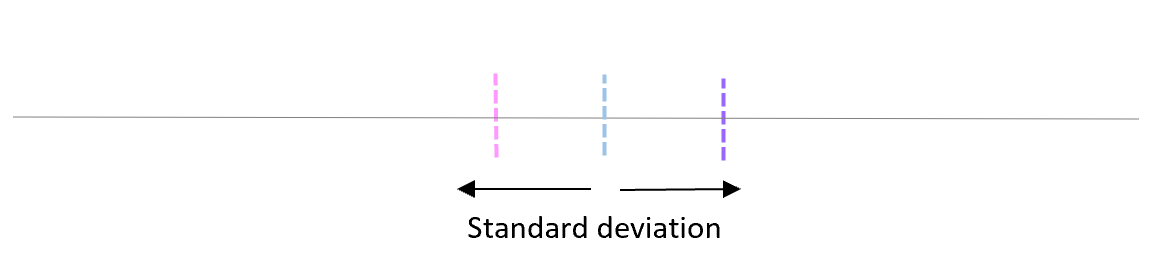
实际计算标准误差的公式是：

标准误差 = s/ √ n

金子：

• s：样本标准差
• n：样本量

使用标准误差有什么意义？

当我们计算给定样本的平均值时，我们实际上并不是要了解该特定样本的平均值，而是要了解该样本所在的较大总体的平均值。

然而，我们使用样本是因为为它们收集数据比为整个群体收集数据要容易得多。

当然，样本均值因样本而异，因此我们使用均值的标准误差来衡量均值估计的精度。

您会注意到，在计算标准误差的公式中，随着样本量 (n) 的增加，标准误差会减小：

标准误差 = s/ √ n

这应该是有道理的，因为较大的样本会减少变异性并增加样本均值更接近真实总体均值的机会。

何时使用标准差与标准误差

如果我们只是想测量数据集中数值的分布，我们可以使用标准差。

但是，如果我们想量化平均值估计的不确定性，我们可以使用平均值的标准误差。

根据您的具体场景和您想要完成的任务，您可以选择使用标准差或标准误差。